假设检验如何选择拒绝域?

007 · 发表于 2025-5-11 12:24

登陆有奖并可浏览互动！

您需要登录才可以下载或查看，没有账号？立即注册

×

新人想问下假设检验拒绝域的选择问题。假设检验遵循小概率事件不可能发生的原理，比如总体均值为100，大样本检测出的均值为1000,经过计算检验统计量后可认为这件事发生概率极低，拒绝原假设。拒绝域选择的原则是检验统计量概率密度函数上发生概率较小的区域吗？卡方检验基本公式用于评估实际频数和理论频数的差异程度，卡方检验拒绝域在右侧，在原假设成立时，如果检验统计量值很大，而理论与实际频数差异程度很大的发生概率极低，则有理由拒绝原假设，那函数左侧的区域为什么不能划为拒绝域，虽然左侧意味着理论与实际频数近乎完全吻合，貌似支持原假设，但这种情况发生的概率也是极低，也就是说原假设成立的情况下实际与理论频数近乎吻合的概率是极低，所以根据小概率原理，在检验统计量接近于0时为什么不拒绝原假设呢？

原文地址：https://www.zhihu.com/question/416079190

感恩由您 · 发表于 2025-5-11 12:25

1 单正态总体

假设 $X=(X_1,\dots,X_n)$ 是一个随机样本，服从正态分布 $N(\mu,\sigma^2)$ 。

考虑以下与参数 $\mu$ 有关的假设检验。其中 $\mu_0$ 与显著性水平 $\alpha$ 为预先设定且已知。
A） $H_0: \mu=\mu_0 \longleftrightarrow H_1: \mu \neq \mu_0$ ；
B） $H_0: \mu \leq \mu_0 \longleftrightarrow H_1: \mu > \mu_0$ ；
C） $H_0: \mu \geq \mu_0 \longleftrightarrow H_1: \mu < \mu_0$ ；

1.1 当 $\sigma^2$ 为已知参数

A） $H_0: \mu=\mu_0 \longleftrightarrow H_1: \mu \neq \mu_0$ ；
已知，样本均值 $\bar{X}$ 是关于 $\mu$ 的一个无偏点估计。并且，从直觉出发，我们容易认同在 $|\bar{X}-\mu_0|$ 很大时应该拒绝零假设 $H_0$ 。所以，我们可以把拒绝域写作如下形式： $D=\{X:|\bar{X}-\mu_0|>A\}$ 。接下来的任务转变为求解临界值 $A$ 。
假设零假设为真，对 $\bar{X}$ 进行变形，可知检验统计量 $Z$ 服从如下分布
$Z=\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{\sigma} \sim N(0,1)\\$
拒绝域的形式可改写为： $D=\left\{X:|Z|>c\right\}$ 。接下来的任务转变为求解 $c$ 。
已知显著性水平为 $\alpha$ ，根据显著性水平的定义 $P\left(|Z|>c \mid H_0\right)=P\left(\left|\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{\sigma}\right|>c \mid H_0\right)=\alpha \\$
从而可以确定 $c=z_{\alpha/2}$ 。拒绝域确定为： $D=\left\{X:\left|\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{\sigma}\right|>z_{\alpha / 2}\right\}$ 。

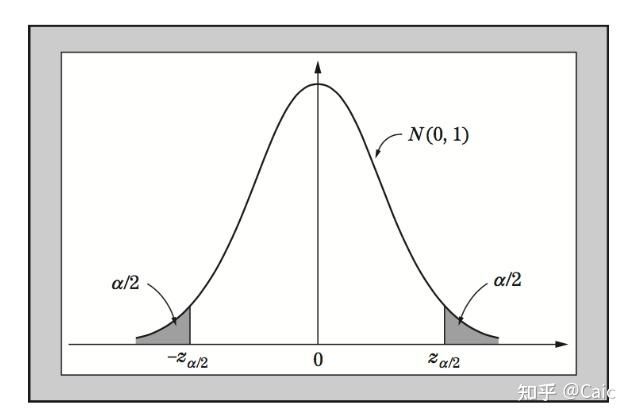
阴影区域为拒绝域（来自清华大学王江典老师课件）

进一步，得到功效函数 $\pi_\varphi(\theta)$ 为
$\begin{aligned} & \pi_1(\mu)=P_\mu\left(\left|\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{\sigma}\right|>z_{\alpha / 2}\right) \\ = & P_\mu\left(\left|\frac{\sqrt{n}\left(\bar{X}-\mu+\mu-\mu_0\right)}{\sigma}\right|>z_{\alpha / 2}\right) \\ = & P_\mu\left(\frac{\sqrt{n}(\bar{X}-\mu)}{\sigma}>z_{\alpha / 2}+\frac{\sqrt{n}\left(\mu_0-\mu\right)}{\sigma}\right) \\ & +P_\mu\left(\frac{\sqrt{n}(\bar{X}-\mu)}{\sigma}<-z_{\alpha / 2}+\frac{\sqrt{n}\left(\mu_0-\mu\right)}{\sigma}\right) \\ = & 1-\Phi\left(z_{\alpha / 2}+\frac{\sqrt{n}\left(\mu_0-\mu\right)}{\sigma}\right)+\Phi\left(-z_{\alpha / 2}+\frac{\sqrt{n}\left(\mu_0-\mu\right)}{\sigma}\right) \end{aligned} \\$
其中， $\Phi(\cdot)$ 为标准正态分布的分布函数。

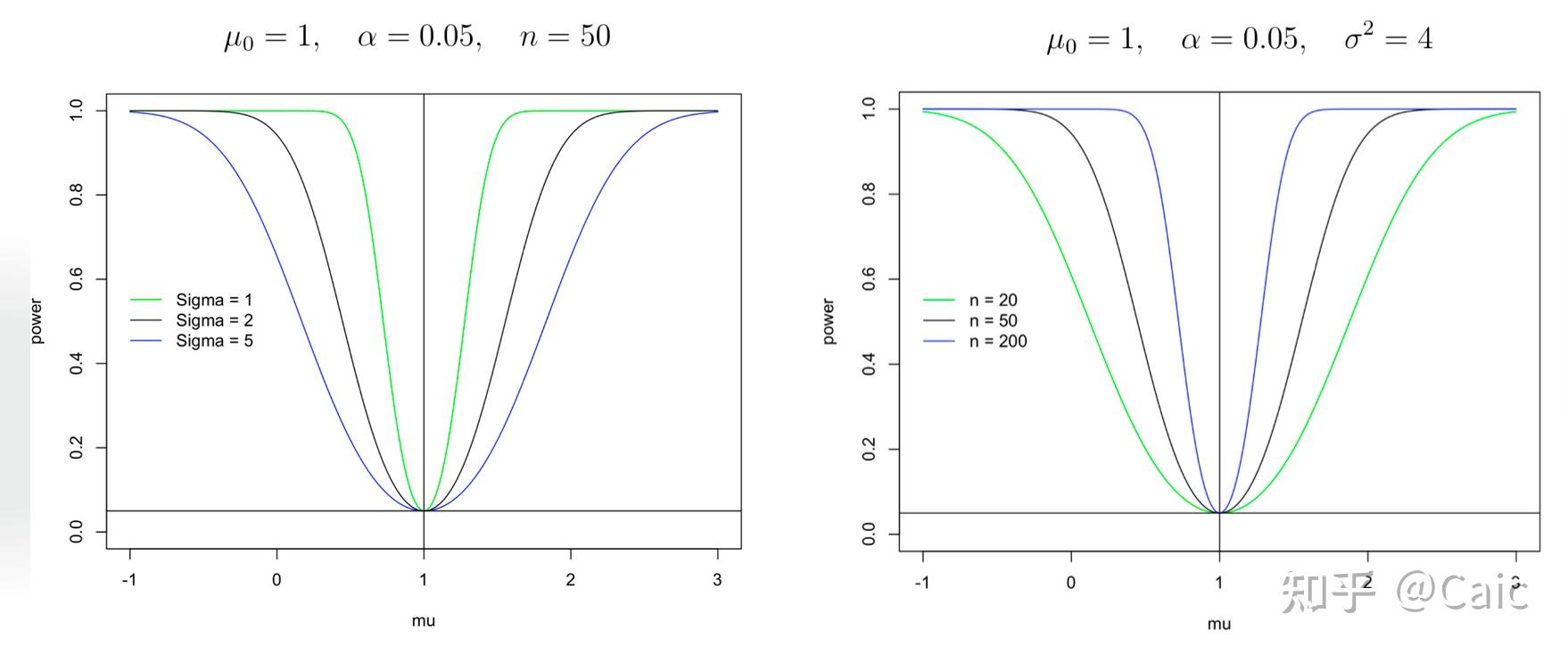
对功效函数的数值模拟（来自清华大学王江典老师课件）

发现该功效函数有两个特别的性质：1) $_1 ( ) = _1(2 _0− )$ ；2) 当 $\mu > \mu_0$ 时， $\pi_1(\mu)$ 单调递增。

此外，还可以引入样本方差 $S^2$ ，构造另一种形式的拒绝域： $D'=\{X:|\bar{X}-\mu_0|/S>A\}$ 。选取另一种检验统计量 $T$ ，当零假设为真时，服从如下分布
$T=\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{S} \sim t_{n-1}\\$
此时，拒绝域形如： $D'=\{X:|T|>c\}$ 。又已知显著性水平为 $\alpha$ ，根据定义
$P\left(|T|>c \mid H_0\right)=P\left(\left|\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{S}\right|>c \mid H_0\right)=\alpha\\$ 从而可以确定 $c=t_{n-1;\alpha/2}$ 。拒绝域为： $D'=\{X:|\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{S}|>t_{n-1;\alpha/2}\}$ 。
此时的功效函数为
$\begin{aligned} & \pi_2(\mu)=P_\mu\left(\left|\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{S}\right|>z_{\alpha / 2}\right) \\ = & P_\mu\left(\left|\frac{\sqrt{n}\left(\bar{X}-\mu+\mu-\mu_0\right)}{S}\right|>z_{\alpha / 2}\right) \\ = & P_\mu\left(\left|\frac{\sqrt{n}(\bar{X}-\mu)}{S}\right|>z_{\alpha / 2}+\frac{\sqrt{n}\left(\mu_0-\mu\right)}{S}\right) \\ & +P_\mu\left(\frac{\sqrt{n}(\bar{X}-\mu)}{S}<-z_{\alpha / 2}+\frac{\sqrt{n}\left(\mu_0-\mu\right)}{S}\right) \end{aligned} \\$
比起第一种来说，非常复杂，但这种功效函数可以适用于 $\sigma^2$ 未知的情形。

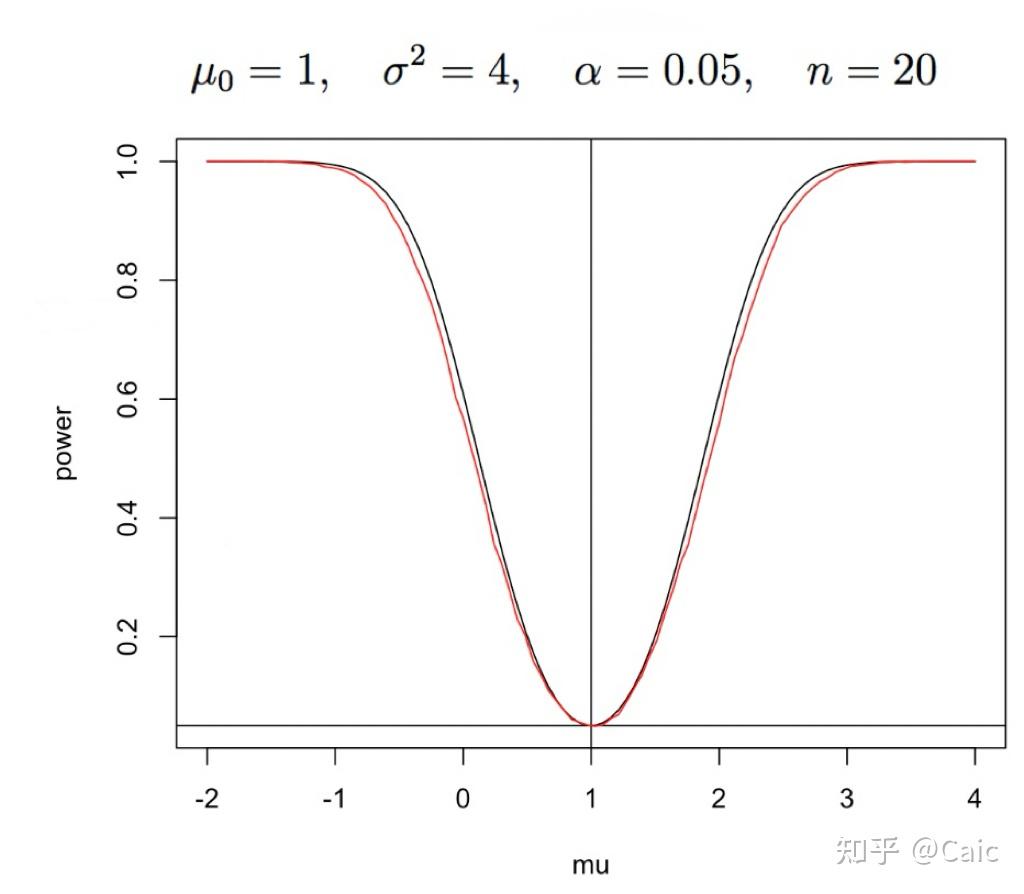
黑：一；红：二（来自清华大学王江典老师课件）

B） $H_0: \mu \leq \mu_0 \longleftrightarrow H_1: \mu > \mu_0$ ；
构造检验统计量为 $Z=\sqrt{n}(\bar{X}-\left.\mu_0\right) / \sigma$ ，所以对应的拒绝域形如： $D=\left\{X: Z>c\right\}$ 。接下来的任务转变为求解 $c$ 。已知显著性水平为 $\alpha$ ，根据显著性水平的定义 $P\left(Z>c \mid \mu=\mu_0\right)=P\left(\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{\sigma}>c \mid \mu=\mu_0\right)=\alpha\\$
从而确定 $c=z_\alpha$ 。拒绝域为： $D_2=\left\{X: \frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{\sigma}>z_\alpha\right\}$ 。
进一步，得到功效函数为
$\begin{aligned} \pi(\mu) & =P_\mu\left(\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{\sigma}>z_\alpha\right) \\ & =P_\mu\left(\frac{\sqrt{n}(\bar{X}-\mu)}{\sigma}>z_\alpha+\frac{\sqrt{n}\left(\mu_0-\mu\right)}{\sigma}\right) \\ & =1-\Phi\left(z_\alpha+\frac{\sqrt{n}\left(\mu_0-\mu\right)}{\sigma}\right) \end{aligned} \\$
是单调递增函数，说明了我们刚刚得到的拒绝域是恰当的。

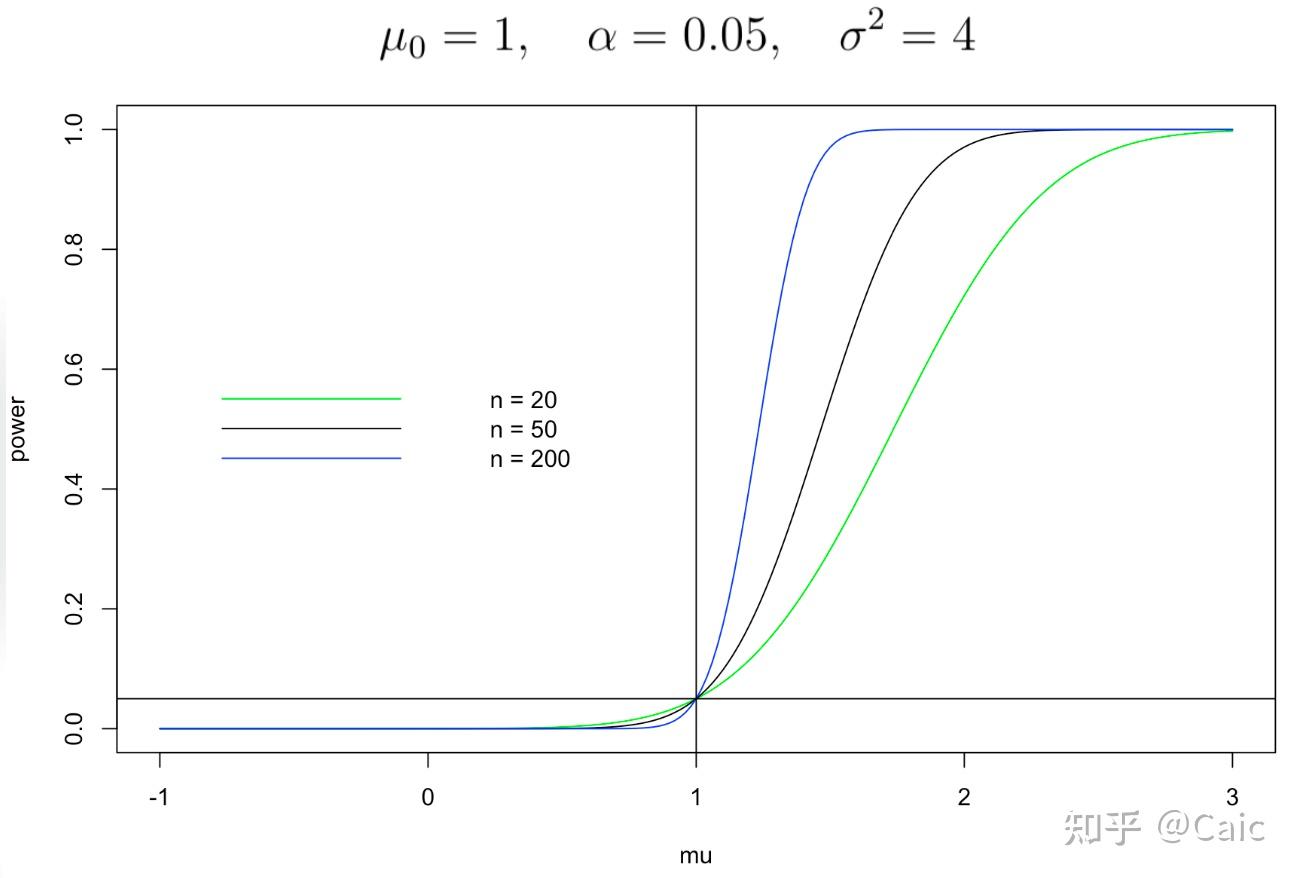
（来自清华大学王江典老师课件）

C） $H_0: \mu \geq \mu_0 \longleftrightarrow H_1: \mu < \mu_0$ ；
此时也取检验统计量为 $Z=\sqrt{n}(\bar{X}-\left.\mu_0\right) / \sigma$ ，经过 B) 中类似的讨论，得到拒绝域 $D_3=\left\{X: \frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{\sigma}<-z_\alpha\right\} \\$

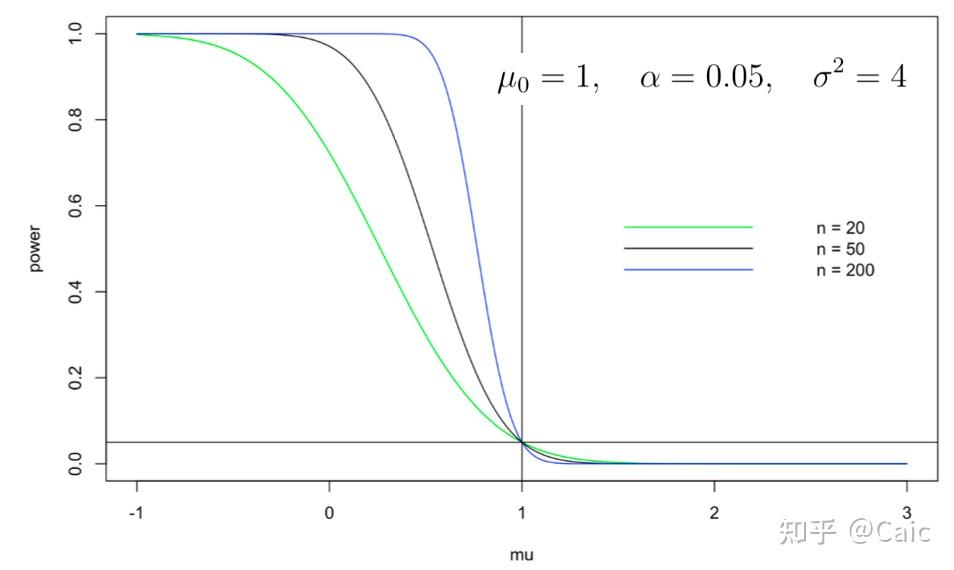
（来自清华大学王江典老师课件）

1.2 当 $\sigma^2$ 为未知参数

此时，采取 1.1 A) 中的处理，将检验统计量中的 $\sigma$ 都替换为样本标准差 $S$ ，为 $T=\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{S} \sim t_{n-1}$ 。此时得到各个检验的拒绝域分别为
A） $D_1=\left\{X:\left|\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{S}\right|>t_{n-1, \alpha / 2}\right\}$ ；
B） $D_2=\left\{X: \frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{S}>t_{n-1, \alpha}\right\}$ ；
C） $D_3=\left\{X: \frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{S}<-t_{n-1, \alpha}\right\}$ ；
以及各自的功效函数为
$\begin{aligned} & \pi_1(\mu)=P_\mu\left(\left|\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{S}\right|>t_{n-1, \alpha / 2}\right) \\ & \pi_2(\mu)=P_\mu\left(\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{S}>t_{n-1, \alpha}\right) \\ & \pi_3(\mu)=P_\mu\left(\frac{\sqrt{n}\left(\bar{X}-\mu_0\right)}{S}<-t_{n-1, \alpha}\right) \end{aligned} \\$

这种基于 $t$ 统计的假设检验，被称为单样本 $t$ 检验 / One Sample $t$ Test。

（来自清华大学王江典老师课件）

考虑以下与参数 $\sigma^2$ 有关的假设检验。其中 $\sigma_0^2$ 与显著性水平 $\alpha$ 为预先设定且已知。
D） $H_0: \sigma^2=\sigma_0^2 \longleftrightarrow H_1: \sigma^2 \neq \sigma_0^2$ ；
E） $H_0: \sigma^2 \leq \sigma_0^2 \longleftrightarrow H_1: \sigma^2>\sigma_0^2$ ；
F） $H_0: \sigma^2 \geq \sigma_0^2 \longleftrightarrow H_1: \sigma^2<\sigma_0^2$ ；

1.3 当 $\mu$ 为未知参数

选取检测统计量为 $T=\frac{(n-1) S^2}{\sigma_0^2} \sim \chi_{n-1}^2\\$
拒绝域应当形如 $\{T>c_1 \text{ or } T<c_2\}$ ， $\{T>c_3\}$ ， $\{T<c_4\}$ 。基于显著性水平的定义 $\alpha=P(X \in D)$ 可以求解得到待定系数的具体取值。从而，每个检验的拒绝域的具体形式如下
D） $D_4=\left\{X: \frac{(n-1) S^2}{\sigma_0^2}<\chi_{n-1,1-\alpha / 2}^2 \text { or } \frac{(n-1) S^2}{\sigma_0^2}>\chi_{n-1, \alpha / 2}^2\right\}$ ；
E） $D_5=\left\{X: \frac{(n-1) S^2}{\sigma_0^2}>\chi_{n-1, \alpha}^2\right\}$ ；
F） $D_6=\left\{X: \frac{(n-1) S^2}{\sigma_0^2}<\chi_{n-1,1-\alpha}^2\right\}$ ；

1.4 当 $\mu$ 为已知参数

设 $S_\mu^2=\sum_{i=1}^n\left(X_i-\mu\right)^2 / n$ ，选取检测统计量为 $\frac{n S_\mu^2}{\sigma_0^2}=\sum_{i=1}^n\left(\frac{X_i-\mu}{\sigma_0}\right)^2 \sim \chi_n^2 \\$
拒绝域应当形如 $\{T>c_1 \text{ or } T<c_2\}$ ， $\{T>c_3\}$ ， $\{T<c_4\}$ 。基于显著性水平的定义 $\alpha=P(X \in D)$ 可以求解得到待定系数的具体取值。从而，每个检验的拒绝域的具体形式如下
D） $D_4=\left\{X: \frac{n S_\mu^2}{\sigma_0^2}<\chi_{n,1-\alpha / 2}^2 \text { or } \frac{n S_\mu^2}{\sigma_0^2}>\chi_{n, \alpha / 2}^2\right\}$ ；
E） $D_5=\left\{X: \frac{n S_\mu^2}{\sigma_0^2}>\chi_{n, \alpha}^2\right\}$ ；
F） $D_6=\left\{X: \frac{n S_\mu^2}{\sigma_0^2}<\chi_{n,1-\alpha}^2\right\}$ ；

这种基于 $\chi^2$ 统计的假设检验，被称为 $\chi^2$ 检验 / $\chi^2$ Test。

（来自清华大学王江典老师课件）

<hr/>2 非正态总体

假设 $X=(X_1,\dots,X_n)$ 是一个随机样本，服从二项分布 $B(1,\theta)$ 。其中参数 $\theta$ 未知。

考虑以下与参数 $\theta$ 有关的假设检验。其中 $\theta_0$ 与显著性水平 $\alpha$ 为预先设定且已知。
A） $H_0: \theta \leq \theta_0 \longleftrightarrow H_1: \theta > \theta_0$ ；
B） $H_0: \theta \geq \theta_0 \longleftrightarrow H_1: \theta < \theta_0$ ；
C） $H_0: \theta=\theta_0 \longleftrightarrow H_1: \theta \neq \theta_0$ ；

2.1 $H_0: \theta \leq \theta_0 \longleftrightarrow H_1: \theta > \theta_0$

假设检验统计量为 $T(\boldsymbol{X})=\sum_{i=1}^n X_i \sim B(n, \theta)$ 。显然， $\bar{X}=T(\boldsymbol{X})/n$ 是一个关于 $\theta$ 的无偏点估计，因此在 $\bar{X}-\theta_0$ 或者 $T(\boldsymbol{X})$ 很大时，我们直觉上会倾向于拒绝零假设，猜测拒绝域形如： $D=\{\boldsymbol{X}:T(\boldsymbol{X})>c\}$ 。
已知，对于非随机检验，显著性水平 $\alpha$ 的定义为
$P\left(T(\boldsymbol{X})>c \mid H_0\right)=P_{\theta_0}(T(\boldsymbol{X})>c)=\alpha\\$
但是对于随机检验来说，在离散的分布下， $T(\boldsymbol{X})>c$ 的概率可能刚好小于 $\alpha$ ， $T(\boldsymbol{X})>c-1$ 的概率又刚好大于 $\alpha$ 。从而不存在一个整数 $c$ 能满足 $P_{\theta_0}(T(\boldsymbol{X})>c)=\alpha$ 。
所以取随机检验函数 $\varphi(\boldsymbol{X})$ 为 $\varphi(\boldsymbol{X})= \begin{cases}1, & T(\boldsymbol{X})>c \\ r, & T(\boldsymbol{X})=c \\ 0, & T(\boldsymbol{X})<c\end{cases} \\$

我们可以这样理解随机检验函数：
当 $T(\boldsymbol{X})<c$ ，判定为接受 $H_0$ ；
当 $T(\boldsymbol{X})>c$ ，判定为拒绝 $H_0$ ；
当 $T(\boldsymbol{X})=c$ ，对 $P(T(\boldsymbol{X})=c)$ 进行调整，抛一枚硬币，正面的概率为 $r$ ，抛到正面就判定为拒绝 $H_0$ 。

得到功效函数 $\pi(\theta)=E_{\theta_0} \varphi(\boldsymbol{X})$ 为
$\pi(\theta)=E_{\theta_0} \varphi(\boldsymbol{X})=P_{\theta_0}(T(\boldsymbol{X})>c)+r P_{\theta_0}(T(\boldsymbol{X})=c)=\alpha\\$
因为 $T(\boldsymbol{X})=\sum_{i=1}^n X_i \sim B(n, \theta)$ ，在取定 $\theta=\theta_0$ 后， $P_{\theta_0}(T(\boldsymbol{X})>c)$ 与 $P_{\theta_0}(T(\boldsymbol{X})=c)$ 的值是可计算的。因此，在确定了临界值 $c$ 的一个具体取值后，根据上式我们可以确定 $r=\frac{\alpha-P_{\theta_0}(T(\boldsymbol{X})>c)}{P_{\theta_0}(T(\boldsymbol{X})=c)}$ 的取值。
例如，如果我们选取一个样本， $n=100$ ， $\theta_0=0.01$ ， $\alpha=0.05$ 。在零假设下有 $T(\boldsymbol{X})=\sum_{i=1}^{100} X_i \sim B(100,0.01)\\$
如果选取 $c=3$ ，那么 $r=\frac{\alpha-P_{\theta_0}(T(\boldsymbol{X})>3)}{P_{\theta_0}(T(\boldsymbol{X})=3)}=\frac{0.05-0.01837404}{0.06099917}=0.518$ 。于是随机检验函数为 $\varphi(\boldsymbol{X})= \begin{cases}1 & T(\boldsymbol{X})>3 \\ 0.518 & T(\boldsymbol{X})=3 \\ 0 & T(\boldsymbol{X})<3\end{cases} \\$

2.2 $H_0: \theta \geq \theta_0 \longleftrightarrow H_1: \theta < \theta_0$

同样地，我们选取检验统计量 $T(\boldsymbol{X})=\sum_{i=1}^n X_i \sim B(n, \theta)$ ，并且拒绝域形如： $D=\{\boldsymbol{X}:T(\boldsymbol{X})<c\}$ 。同样有随机检验函数形如
$\varphi(\boldsymbol{X})= \begin{cases}1, & T(\boldsymbol{X})<c \\ r, & T(\boldsymbol{X})=c \\ 0, & T(\boldsymbol{X})>c\end{cases} \\$
得到功效函数 $\pi(\theta)=E_{\theta_0} \varphi(\boldsymbol{X})=P_{\theta_0}(T(\boldsymbol{X})<c)+r P_{\theta_0}(T(\boldsymbol{X})=c)=\alpha\\$
样本取定后，这些都是可计算的。

2.3 $H_0: \theta=\theta_0 \longleftrightarrow H_1: \theta \neq \theta_0$

仍然选取检验统计量 $T(\boldsymbol{X})=\sum_{i=1}^n X_i \sim B(n, \theta)$ ，拒绝域： $D=\{\boldsymbol{X}:T(\boldsymbol{X})<c_1\text{ or }T(\boldsymbol{X})>c_2\}$ 。
随机检验函数形如 $\varphi(\boldsymbol{X})= \begin{cases}1, & T(\boldsymbol{X})<c_1 \text { or } T(\boldsymbol{X})>c_2 \\ r_1, & T(\boldsymbol{X})=c_1 \\ r_2, & T(\boldsymbol{X})=c_2 \\ 0, & c_1<T(\boldsymbol{X})<c_2\end{cases} \\$
根据显著性水平 $\alpha$ 的定义
$\begin{gathered} P_{\theta_0}\left(T(\boldsymbol{X})<c_1\right)+r_1 P_{\theta_0}\left(T(\boldsymbol{X})=c_1\right)=\alpha / 2 \\ P_{\theta_0}\left(T(\boldsymbol{X})>c_2\right)+r_2 P_{\theta_0}\left(T(\boldsymbol{X})=c_2\right)=\alpha / 2 \end{gathered} \\$
在样本取定后，这些都是可计算的。
<hr/>3 双正态总体

假设 $X=(X_1,\dots,X_m)$ 是一个随机样本，服从正态分布 $N(\mu_1,\sigma_1^2)$ ； $Y=(Y_1,\dots,Y_n)$ 也是一个随机样本，服从正态分布 $N(\mu_2,\sigma_2^2)$ 。

考虑以下与参数 $\mu_1-\mu_2$ 有关的假设检验。其中 $\mu_0$ 与显著性水平 $\alpha$ 为预先设定且已知。
A） $H_0: \mu_1-\mu_2=\mu_0 \longleftrightarrow H_1: \mu_1-\mu_2 \neq \mu_0$ ；
B） $H_0: \mu_1-\mu_2 \leq \mu_0 \longleftrightarrow H_1: \mu_1-\mu_2 > \mu_0$ ；
C） $H_0: \mu_1-\mu_2 \geq \mu_0 \longleftrightarrow H_1: \mu_1-\mu_2 < \mu_0$ ；

3.1 $\sigma_1^2$ 和 $\sigma_2^2$ 均已知

先考虑双边检验 $H_0: \mu_1-\mu_2=\mu_0 \longleftrightarrow H_1: \mu_1-\mu_2 \neq \mu_0$ 。显然， $\bar{X}-\bar{Y}$ 是一个关于 $\mu_1-\mu_2$ 的无偏点估计。并且，当 $|\bar{X}-\bar{Y}-\mu_0|$ 很大时，我们会在直觉上倾向于拒绝零假设。并且此时拒绝域应当形如： $D=\{(\boldsymbol{X};\boldsymbol{Y}):|\bar{X}-\bar{Y}-\mu_0|>c\}$ 。
具体地，我们将选取检验统计量为
$U=\frac{\bar{X}-\bar{Y}-\mu_0}{\sqrt{\sigma_1^2 / m+\sigma_2^2 / n}} \sim N(0,1)\\$
此时的拒绝域为： $D=\{(\boldsymbol{X};\boldsymbol{Y}):|U(\boldsymbol{X},\boldsymbol{Y})|>c\}$ 。
根据显著性水平的定义有
$\alpha=P_\theta\left(|U|>c \mid H_0\right)=P\left(\left|\frac{\bar{X}-\bar{Y}-\mu_0}{\sqrt{\sigma_1^2 / m+\sigma_2^2 / n}}\right|>c \mid H_0\right)\\$
所以，可以确定 $c=z_{\alpha/2}$ 。另外两种检验都可以通过类似的方法确定拒绝域。总体结果如下：
A） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\left|\frac{\bar{X}-\bar{Y}-\mu_0}{\sqrt{\sigma_1^2 / m+\sigma_2^2 / n}}\right|>z_{\alpha/2}\}$ ；
B） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\frac{\bar{X}-\bar{Y}-\mu_0}{\sqrt{\sigma_1^2 / m+\sigma_2^2 / n}}>z_{\alpha}\}$ ；
C） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\frac{\bar{X}-\bar{Y}-\mu_0}{\sqrt{\sigma_1^2 / m+\sigma_2^2 / n}}<-z_{\alpha}\}$ ；

3.2 $\sigma_1^2=\sigma_2^2=\sigma^2$ 但未知

这种情况被称为双样本 $t$ 检验 / Two Sample $t$ Test。选取检验统计量 $T$ 为 $T=\frac{\bar{X}-\bar{Y}-\mu_0}{\sqrt{\frac{(m-1) S_X^2+(n-1) S_Y^2}{m+n-2}\left(\frac{1}{m}+\frac{1}{n}\right)}} \sim t_{m+n-2} \quad \mid \mu_1-\mu_2=\mu_0\\$
同样地，按照显著性水平的定义，可以得到各个检验的拒绝域分别为
A） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\left|T\right|>t_{m+n-2,\alpha/2}\}$ ；
B） $D=\{(\boldsymbol{X};\boldsymbol{Y}):T>t_{m+n-2,\alpha}\}$ ；
C） $D=\{(\boldsymbol{X};\boldsymbol{Y}):T<-t_{m+n-2,\alpha}\}$ ；

（来自清华大学王江典老师课件）

3.3 $\sigma_1^2 \neq \sigma_2^2$ 且未知

选取检验统计量 $T_*$ 为 $T_*=\frac{(\bar{X}-\bar{Y})-u_0}{\sqrt{S_X^2 / m+S_Y^2 / n}} \\$
在零假设成立时， $T_*$ 不服从 $t$ 分布，只能采用渐进的方法，近似于 $t_r$ 分布。其中，自由度 $r$ 为
$\left(\frac{S_X^2}{m}+\frac{S_Y^2}{n}\right)^2 /\left[\frac{S_X^4}{m^2(m-1)}+\frac{S_Y^4}{n^2(n-1)}\right] \\$
对上式四舍五入取最接近的整数。

现在，考虑以下与参数 $\sigma_2^2/\sigma_1^2$ 有关的假设检验。其中显著性水平 $\alpha$ 为预先设定且已知。
D） $H_0: \sigma_2^2/\sigma_1^2=1 \longleftrightarrow H_1: \sigma_2^2/\sigma_1^2 \neq 1$ ；
E） $H_0: \sigma_2^2/\sigma_1^2\leq1 \longleftrightarrow H_1: \sigma_2^2/\sigma_1^2 > 1$ ；
F） $H_0: \sigma_2^2/\sigma_1^2\geq1 \longleftrightarrow H_1: \sigma_2^2/\sigma_1^2 < 1$ ；

3.4 $\mu_1$ 和 $\mu_2$ 未知

选取检验统计量 $F$ 为
$F=\frac{S_Y^2}{S_X^2} \sim F_{n-1, m-1} \quad \mid H_0\\$
拒绝域形如： $D=\{(\boldsymbol{X};\boldsymbol{Y}):F<c_1 \text{ or } F>c_2\}$ 。
根据显著性水平的定义
$\alpha=P_\theta\left(\frac{S_Y^2}{S_X^2}<c_1 \text { or } \frac{S_Y^2}{S_X^2}>c_2 \mid H_0\right) \\$
所以，选取 $c_1=F_{n-1, m-1,1-\alpha / 2}$ 和 $c_2=F_{n-1, m-1, \alpha / 2}$ 。从而可以确定拒绝域的具体范围。同样地，另外两个假设检验也可以通过选取该检验统计量来求解拒绝域，总的结果如下：
D） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\frac{S_Y^2}{S_X^2}<F_{n-1, m-1,1-\alpha / 2} \text { or } \frac{S_Y^2}{S_X^2}>F_{n-1, m-1, \alpha / 2}\}$ ；
E） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\frac{S_Y^2}{S_X^2}>F_{n-1, m-1,\alpha} \}$ ；
F） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\frac{S_Y^2}{S_X^2}<F_{n-1, m-1,1-\alpha}\}$ ；

3.5 $\mu_1$ 和 $\mu_2$ 已知

设 $S_{X *}^2=\frac{1}{m} \sum_{i=1}^m\left(X_i-\mu_1\right)^2$ 和 $S_{Y *}^2=\frac{1}{n} \sum_{i=1}^n\left(Y_i-\mu_2\right)^2$ 。此时，选取检验统计量 $F_*$ 为
$F_*=\frac{S_{Y *}^2}{S_{X *}^2} \sim F_{n, m} \quad \mid H_0\\$
使用与 3.3 中一样的方法，得到各个假设检验的拒绝域如下：
D） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\frac{S_{Y *}^2}{S_{X *}^2}<F_{n, m,1-\alpha / 2} \text { or } \frac{S_{Y *}^2}{S_{X *}^2}>F_{n, m, \alpha / 2}\}$ ；
E） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\frac{S_{Y *}^2}{S_{X *}^2}>F_{n, m,\alpha} \}$ ；
F） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\frac{S_{Y *}^2}{S_{X *}^2}<F_{n, m,1-\alpha}\}$ ；

（来自清华大学王江典老师课件）

3.6 示例

EX1：为研究正常成年男女血液红细胞平均数的差别，检验某地正常成年男子156人，女子74人，计算得到男女红细胞的平均数和样本标准差分别为：男， $\bar{X}=465.13$ 万 $/ \mathrm{mm}^3$ ， $S_X=54.80$ 万 $/ \mathrm{mm}^3$ ；男， $\bar{Y}=422.16$ 万 $/ \mathrm{mm}^3$ ， $S_Y=49.20$ 万 $/ \mathrm{mm}^3$ 。假定正常男女红细胞数分别服从正态分布，且方差相同（但未知）。检验正常成年人红细胞数是否与性别有关（取显著水平 $= 0.01$ ）。
转化为统计学语言，即考虑如下假设检验： $H_0: \mu_1-\mu_2=0 \longleftrightarrow H_1: \mu_1-\mu_2 \neq 0$ 。
根据 3.2 中的讨论，易知此时的拒绝域为： $D=\{(\boldsymbol{X};\boldsymbol{Y}):\left|\frac{\bar{X}-\bar{Y}}{\sqrt{\frac{(m-1) S_X^2+(n-1) S_Y^2}{m+n-2}\left(\frac{1}{m}+\frac{1}{n}\right)}}\right|>t_{m+n-2,\alpha/2}\}\\$
直接带入题给数据，得到
$|T|=\left|\frac{\bar{X}-\bar{Y}}{\sqrt{\frac{(m-1) S_X^2+(n-1) S_Y^2}{m+n-2}\left(\frac{1}{m}+\frac{1}{n}\right)}}\right|=5.74>2.598\\$
拒绝零假设，即正常成年人红细胞数确实与性别有关，P 值为 $p=P\left(\left|t_{228}\right|>5.74\right)=3 e-08<0.001$ 。

EX2：为了考察一种安眠药的效果，记录了 $n$ 个失眠患者服药前的每晚睡眠时间 $X=\{X_1,\dots,X_n\}$ 和服用此安眠药后的每晚睡眠时间 $Y=\{Y_1,\dots,Y_n\}$ 。其中 $(X_i,Y_i)$ 是第 $i$ 个患者不服用安眠药和服用安眠药每晚的睡眠时间，请分析该安眠药的效果。
此时， $X$ 和 $Y$ 是两个不独立的随机样本，不能直接套用之前的讨论。设 $Z_i=X_i-Y_i \sim N(\mu,\sigma^2)$ ，于是将问题转化为如下假设检验： $H_0: \mu=0 \longleftrightarrow H_1: \mu \neq 0$ 。采用 1.2 中讨论的结果，拒绝域为：
$D=\left\{\left(Z_1, \cdots, Z_n\right):\left|\sqrt{n} \bar{Z} / S_Z\right|>t_{n-1, \alpha / 2}\right\}\\$

EX3：有两台测量材料中某种金属含量的光谱仪A和B，为鉴定它们的质量有无显著差异，对金属含量不同的 9 件材料样品进行测量，得到 9 对观测值为

（来自清华大学王江典老师课件）

根据试验结果，在 $= 0.01$ 下，能否判断这两台光谱仪的质量有无显著差异？
此时，仍然认为 $X$ 和 $Y$ 是两个不独立的随机样本，设 $Z_i=X_i-Y_i \sim N(\mu,\sigma^2)$ ，将问题转化为如下假设检验： $H_0: \mu=0 \longleftrightarrow H_1: \mu \neq 0$ 。拒绝域为： $D=\left\{\boldsymbol{Z}: \sqrt{9}|\bar{Z}| / S_Z \mid>t_{8, \alpha / 2}\right\}$ 。
带入数据： $\bar{Z}=0.06, S_Z^2=0.01505, S_Z=0.12268, t_{8,0.005}=3.3554$ 。
$\sqrt{9}|\bar{Z}| / S_Z \mid=(3 \times 0.06) / 0.12268=1.47<3.3554\\$
接受零假设，即认为这两台光谱仪的质量没有显著差异，P 值为 $p=P\left(\sqrt{9}|\bar{Z}| / S_Z|>1.47| H_0\right)=0.18$ 。

EX4：有两批样本大小皆为 6 的电子器材，分别测量其电阻，得到两组数据：均值 $\bar{ } = 0.14$ 和 $\bar{Y} = 0.139$ ；样本标准差 $_ = 0.0026$ 和 $_ = 0.0024$ 。假设这两组电阻数据分别服从不同的正态分布，方差皆未知且两组样本独立。问：两批电子器材的电阻是否相同？取 $= 0.05$ 。
尽管方差均未知，但可以先检验两组方差是否相同，选取假设检验： $H_0: \sigma_2^2=\sigma_1^2 \longleftrightarrow H_1: \sigma_2^2 \neq \sigma_1^2$ 。根据 3.4 中的讨论，拒绝域为： $D=\{(\boldsymbol{X};\boldsymbol{Y}):\frac{S_Y^2}{S_X^2}<F_{n-1, m-1,1-\alpha / 2} \text { or } \frac{S_Y^2}{S_X^2}>F_{n-1, m-1, \alpha / 2}\}$ 。
带入题给数据 $S_Y^2 / S_X^2=0.0024^2 / 0.0026^2=0.85$ ， $F_{5,5,0.975}=0.14$ ， $F_{5,5,0.025}=7.15$ 。
$F_{5,5,0.975}<S_Y^2 / S_X^2<F_{5,5,0.025}\\$
接受零假设，即认为两个样本的方差相同但未知。
此时，考虑电阻均值，选取假设检验： $H_0^{\prime}: \mu_1=\mu_2 \longleftrightarrow H_1^{\prime}: \mu_1 \neq \mu_2$ 。根据 3.2 中的讨论，拒绝域为
$D=\{(\boldsymbol{X};\boldsymbol{Y}):\left|\frac{\bar{X}-\bar{Y}}{\sqrt{\frac{(m-1) S_X^2+(n-1) S_Y^2}{m+n-2}\left(\frac{1}{m}+\frac{1}{n}\right)}}\right|>t_{m+n-2,\alpha/2}\}\\$
带入题给数据： $|T|=0.6928<2.228=t_{10,0.025}$ 。接受零假设，认为两批电子器材的电阻相同。
<hr/>4 基于大样本定理的假设检验

假设 $X=(X_1,\dots,X_n)$ 是一个随机样本，服从分布 $F$ ：期望的分布均值为 $\mu$ ，分布方差为 $\sigma^2$ ；样本均值为 $\bar{X}_n=\sum_{i=1}^n X_i / n$ ，样本方差为 $S^2=\sum_{i=1}^n\left(X_i-\bar{X}\right)^2 /(n-1)$ 。考虑以下两个统计量的分布。
1） $\sqrt{n}\left(\bar{X}_n-\mu\right) / \sigma$ ：
如果 $F=N\left(\mu, \sigma^2\right)$ ，那么 $\sqrt{n}\left(\bar{X}_n-\mu\right) / \sigma \sim N(0,1)$ ；
如果 $F \neq N\left(\mu, \sigma^2\right)$ ，那么在 $n$ 足够大时，根据 CLT 有 $\sqrt{n}\left(\bar{X}_n-\mu\right) / \sigma \stackrel{d}{\rightarrow} N(0,1)$ ；
2） $\sqrt{n}\left(\bar{X}_n-\mu\right) / S$ ：
如果 $F=N\left(\mu, \sigma^2\right)$ ，那么 $\sqrt{n}\left(\bar{X}_n-\mu\right) / S \sim t_{n-1}$ ；
如果 $F \neq N\left(\mu, \sigma^2\right)$ ，那么在 $n$ 足够大时，根据 CLT 和 Slutsky Thm 有 $\sqrt{n}\left(\bar{X}_n-\mu\right) / S \stackrel{d}{\rightarrow} N(0,1)$ ；

4.1 当 $\sigma_1^2$ 和 $\sigma_2^2$ 未知时，对 $\mu_1-\mu_2$ 进行假设检验

在 3.3 中我们曾简单讨论过，此时选取检验统计量 $T_*$ 为 $T_*=\frac{(\bar{X}-\bar{Y})-u_0}{\sqrt{S_X^2 / m+S_Y^2 / n}} \\$
在零假设成立时， $T_*$ 不服从任何已知的分布，所以在 3.3 中我们采取了渐进分布来处理。
而当 $n$ 足够大时，我们可以采取 CLT 和 Slutsky Thm 得到 $T_*$ 在大样本下近似为 $N(0,1)$ 分布
$\frac{(\bar{X}-\bar{Y})-\left(u_1-u_2\right)}{\sqrt{S_X^2 / m+S_Y^2 / n}}=\frac{(\bar{X}-\bar{Y})-\left(u_1-u_2\right)}{\sqrt{\sigma_1^2 / m+\sigma_2^2 / n}} \cdot \frac{\sqrt{\sigma_1^2 / m+\sigma_2^2 / n}}{\sqrt{\sigma_1^2 / m+\sigma_2^2 / n}} \underset{m, n \rightarrow \infty}{\longrightarrow} N(0,1)\\$
在零假设下， $u_1-u_2=u_0$ 。同样地，我们也可以得出大样本下的拒绝域为：
A） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\left|\frac{\bar{X}-\bar{Y}-\mu_0}{\sqrt{S_X^2 / m+S_Y^2 / n}}\right|>z_{\alpha/2}\}$ ；
B） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\frac{\bar{X}-\bar{Y}-\mu_0}{\sqrt{S_X^2 / m+S_Y^2 / n}}>z_{\alpha}\}$ ；
C） $D=\{(\boldsymbol{X};\boldsymbol{Y}):\frac{\bar{X}-\bar{Y}-\mu_0}{\sqrt{S_X^2 / m+S_Y^2 / n}}<-z_{\alpha}\}$ ；

EX：3.6 中的 EX1，但方差未必相同，检验正常成年人红细胞数是否与性别有关（取显著水平 $= 0.01$ ）。
选取检验为： $H_0: \mu_1-\mu_2=0 \longleftrightarrow H_1: \mu_1-\mu_2 \neq 0$ ，此时不再是 $t$ 检验。
$D=\{(\boldsymbol{X};\boldsymbol{Y}):\left|\frac{\bar{X}-\bar{Y}-\mu_0}{\sqrt{S_X^2 / m+S_Y^2 / n}}\right|>z_{\alpha/2}\}\\$
带入题给数据： $\bar{X}=465.13, \bar{Y}=422.16, S_X=54.80, S_Y=49.20,z_{(0.005)}=2.576$ 。
$\left|T_*\right|=\left|\frac{422.16-465.13}{\sqrt{54.80^2 / 176+49.20^2 / 74}}\right|=6.09>2.576\\$
拒绝零假设，P 值为 $p=P(|N(0,1)|>6.09)=1 e-09<0.001$ 。

4.2 对 $B(1,\theta)$ 的参数 $\theta$ 进行假设检验

假设 $X=(X_1,\dots,X_n)$ 是一个随机样本，服从伯努利分布 $B(1,\theta)$ 。给定显著性水平 $\alpha$ 。
根据 CLT 有
$\frac{\sqrt{n}(\bar{X}-\theta)}{\sqrt{\theta(1-\theta)}} \underset{n \rightarrow \infty}{\stackrel{d}{\longrightarrow}} N(0,1)\\$
在零假设下 $U=\frac{\sqrt{n}\left(\bar{X}-\theta_0\right)}{\sqrt{\theta_0\left(1-\theta_0\right)}} \underset{n \rightarrow \infty}{\stackrel{d}{\longrightarrow}} N(0,1)\\$
从而得到各个假设检验下的拒绝域为
A） $H_0^{\prime}: \theta = \theta_0 \leftrightarrow H_1^{\prime}: \theta\neq\theta_0, \quad D_1=\left\{\boldsymbol{X}: |U|>z_\alpha/2\right\}$ ；；
B） $H_0^{\prime}: \theta \leq \theta_0 \leftrightarrow H_1^{\prime}: \theta>\theta_0, \quad D_2=\left\{\boldsymbol{X}: U>z_\alpha\right\}$ ；
C） $H_0^{\prime \prime}: \theta \geq \theta_0 \leftrightarrow H_1^{\prime \prime}: \theta<\theta_0, \quad D_3=\left\{\boldsymbol{X}: U<-z_\alpha\right\}$ ；

4.3 对 $P(\theta)$ 的参数 $\theta$ 进行假设检验

假设 $X=(X_1,\dots,X_n)$ 是一个随机样本，服从柏松分布 $P(\theta)$ 。给定显著性水平 $\alpha$ 。
根据 CLT 有
$\frac{\sqrt{n}(\bar{X}-\theta)}{\sqrt{\theta}} \underset{n \rightarrow \infty}{\stackrel{d}{\longrightarrow}} N(0,1)\\$
在零假设下 $U_0=\frac{\sqrt{n}\left(\bar{X}-\theta_0\right)}{\sqrt{\theta_0}} \underset{n \rightarrow \infty}{\stackrel{d}{\longrightarrow}} N(0,1)\\$
从而得到各个假设检验下的拒绝域为
A） $H_0^{\prime}: \theta = \theta_0 \leftrightarrow H_1^{\prime}: \theta\neq\theta_0, \quad D_1=\left\{\boldsymbol{X}: |U_0|>z_\alpha/2\right\}$ ；；
B） $H_0^{\prime}: \theta \leq \theta_0 \leftrightarrow H_1^{\prime}: \theta>\theta_0, \quad D_2=\left\{\boldsymbol{X}: U_0>z_\alpha\right\}$ ；
C） $H_0^{\prime \prime}: \theta \geq \theta_0 \leftrightarrow H_1^{\prime \prime}: \theta<\theta_0, \quad D_3=\left\{\boldsymbol{X}: U_0<-z_\alpha\right\}$ ；

4.4 自举法 / Bootstrapping Method

Bootstrapping Method 是一种统计学上的重采样技术，通过从原始样本中随机重复抽取，来构造伪样本，从而估计一个统计量的分布，并进一步评估估计值的变异性和置信区间。
无需依赖大样本量或正态分布的假设，在小样本研究或非参数研究中特别有用。

（来自清华大学王江典老师课件）

EX：1882年，西蒙·纽科姆做了一个测量光速的实验。下面的数字代表了光从波托马克河西岸的迈尔堡到达3721米外华盛顿纪念碑脚下的一面固定镜子所花费的测量时间。

（来自清华大学王江典老师课件）

在给出数据的单位中，目前公认的“真实”光速是33.02，请分析这些数据是否支持目前公认的光速。
运用 Bootstrapping Method 一般遵从以下流程：随机抽样若干个观察值，并进行替换，得到伪样本，计算 P 值。
本题采用的 R 语言代码如下，感兴趣的知友可以跑一下：
> speed <- c(28, -44, 29, 30, 26, 27, 22, 23, 33, 16, 24, 29, 24, 40, 21, 31, 34, -2, 25, 19)
> hist(speed)

> newspeed <- speed - mean(speed) + 33.02
> mean(newspeed)

> bstrap <~ cO
> for (i in 1:1000){
+ newsample <- sample(newspeed, 20, replace=T)
+ bstrap <- c(bstrap, mean(newsample))}
> hist(bstrap)

> (sum(bstrap < 21.75) + sum(bstrap > 44.29))/1000更多关于 Bootstrapping Method 的例子，可以参考以下知乎回答：
商胜彭：Bootstrapping算法（附python代码）什么是Bootstrapping？

大力水手 · 发表于 2025-5-11 12:25

假设检验研究的问题包括：

先回忆一个双侧检验的例子：

图1

这个例子实际就是这样一个意思：什么情况下我们认为新机床加工的零件是合格的？什么情况下我们又认为是不合格的？从图1中我们看到，当新加工的零件平均值与总体均值的误差等于0.005mm的时候，我们认为这批新零件不合格，理由是什么呢？就是因为这个差值导致样本统计量的检验结果落入了拒绝域。从图1我们还可以看到，假如将-2.83换成-1.96,样本均值就会从0.076变成另外一个数字，我们假设是0.078,也就是说，
当样本与总体的均值差<0.003mm的时候，我们都认为新产品是合格的。
上述过程可以简单总结成一句话：只要新产品和老产品的平均值的差别不要大于0.003mm,我们都认为新产品是合格的。大于0.003mm是一个小概率事件（5%），结果在图1中真的发生了，所以我们只好认为新产品是不合格的。
这就好比一个男孩子对一个女孩子说：我今天晚上一定请你去吃海鲜（原假设H0）,除非有另外一个更漂亮的女孩子请我看电影（可能性小于%5,即显著性水平，就是可以推翻原假设的可能性的大小），结果真有一个更漂亮的女孩子请他看电影（事情进入了拒绝域），于是就吃不了海鲜（拒绝原假设）。
再看一个单侧检验的例子：
根据过去大量资料，某厂生产的灯泡的使用寿命服从正态分布N~(1020，1002)。现从最近生产的一批产品中随机抽取16只，测得样本平均寿命为1080小时。试在0.05的显著性水平下判断这批产品的使用寿命是否有显著提高？(a＝0.05)

图2

我们注意到，原假设H0是小于等于1020，也就是新灯泡的使用寿命没有提高甚至降低。那什么情况下可以认为灯泡使用寿命提高了呢？我们认为，新灯泡使用寿命提高的可能性要小于5%，从图2可以看到，当新灯泡的平均寿命比原灯泡的平均寿命大于60（1080-1020）小时的时候，落入了原假设的拒绝域，因此我们可以拒绝原假设，从而认为灯泡寿命有了明显提高。这里面还包含了另一层意思，假设1.645对应的新灯泡的平均值（x平均）是1050，也就是说，只有新灯泡寿命超过原灯泡30小时以上，才可以认为使用寿命有显著提高。
这种情况下为什么不能采用双侧检验呢？很简单，因为新灯泡的平均寿命比原灯泡的平均寿命小于60（960-1020）小时的时候，也会落入拒绝域，而这种情况是明显不可以认为新灯泡的平均寿命有了提高的。

感恩由您 · 发表于 2025-5-11 12:26

通俗的说说吧：
比如现在有一个假设检验的原假设：小猫大于等于小狗。该检验的检验规则是：当检验p值小于等于显著性水平的时候拒绝原假设。然后设置显著性水平a=0.05，假设你通过数据检验出来的检验统计量所对应的p=0.031。
所以结论是：在0.05的显著性水平下，拒绝小猫大于等于小狗的原假设，接受备择假设小狗大于小猫。但是当你说这个结论的时候，你有3.1%的错误犯错。即真实的情况其实有很小的可能是小猫大于等于小狗。至于拒绝域也就是显著性水平，就是你所能够接受的犯错的最大概率值，即5%。
如果你把显著性水平设定到0.01，那在这个显著性水平下，你得到的结论就是小猫大于等于小狗这个结论了。
所以，其实你可以把拒绝域的选择看作是对第一类统计错误的容忍度，对于卡方分布来说，你偏左点就是能接受错误概率更高的结论，往右点，就是更希望得到更“严格”的结论。

继续前进 · 发表于 2025-5-11 12:26

题主，你上一个问题“卡方检验为什么是单侧？”就了邀请我，我也认真答了。链接：
卡方检验为什么是单侧？可是你对我的答案没有提供反馈，而是继续提问“假设检验如何选择拒绝域？”结果我仔细一看，这俩根本就是同一个问题啊！我寻思着可能是我上一个回答不合你意呗，但你又邀请我回答这个问题，这让我有点摸不着头脑。您这番操作，难道是“再给你一次机会，好好表现”的意思么？
<hr/>上面是玩笑话。网络嘛，你问你的我答我的，本来就是两不相干的事情。不过我发现有些答案貌似并不理解你的问题。但是没关系，我懂你啊！虽然我不是很确定您是否看明白了我上一个回答。
以下是回答的内容：
您的问题描述是想说：用chi-squared test检测observed frequencies和theoretical frequencies时，如果两者相差很大——这是一件小概率事件——那么chi-squared statistic的值会很大，最终会落到右侧的拒绝域；同样，observed frequencies和theoretical frequencies“恰好相等”的情形在您看来也是一件极小概率的事件。为什么同样一件极小概率的事件，不能同样地被划入拒绝域中呢？
咱们把这件事掰开来，一点一点给它理顺了吧：
首先，什么是假设检验（testing）？
统计学家要test一个假说是否成立，是这么一个过程：

明确一个随机事件，及这个随机事件所有可能的结果outcomes。
使用一个随机变量random variable来代表这个随机事件，并根据该随机事件可能出现的结果相应地对随机变量赋值。比如说，你同时抛出两个筛子（一次随机事件），记出现数字之和为事件的结果。你多次重复做这件事，把每次的数字都记录下来（随机变量），就完成了统计学家称之为的一次“从随机事件到随机变量的映射”。
每个随机变量都是有一个对应的概率密度函数pdf描述它的行为。比如扔两个筛子，最有可能出现的数字是7，最没可能出现的是2和12。当你将每一种情况都列清楚了，你就得到了这个随机变量的概率密度函数，或者说它的分布。
统计学家想知道随机变量 $x$ 等不等于常数 $a$ ，他们就要做test，记为， $H_{0}: \quad x=a$ 。因为 $x$ 作为一个随机变量，我们是知道它的分布的，所以当 $a$ 在 $x$ 的分布中处于“很不可能发生”的位置时，我们就“有信心”拒绝原假设 $H_{0}$ ，即我们说 $x$ 不太可能等于 $a$ 。
以上都是背景知识，你要是学过统计就不用看了。
你所纠结的“为什么检验是单侧”或“拒绝域为什么只选在右侧而不是左侧”，其实本质上不是什么原则性问题。很多tests之所以是双侧的，根本原因是因为，大部分的随机变量都是定义在实数轴 $R$ 上的，其“运动”是一维的。假如定义随机变量在实虚数共同构成的二维平面上，一个test是N侧的，这也是有可能的。所以从这一点来说，你的思考的出发点是有根据的。
但是，你在思考更高层次的问题时，把最基本的问题搞错了。我希望这次能引起到你的注意：

卡方检验之所以不能是双侧的，跟“实际频率与理论频率完全吻合是一个小概率事件”没有关系，跟卡方分布不同自由度的“形状”也没有关系。
卡方检验之所以不能是双侧的，是因为这个test的原假设 $H_{0}:\quad x=0$ 将检验点设在了这个分布的端点处。你明白吗？我上一个回答的核心也是这句话。卡方分布的起始点在零点处，而卡方检验的原假设要检测的点恰好也是零点处。所以这个检验中，备择假设只剩下了一种情况。所以，这个检测是一个单侧检测。
以上。

同花顺 · 发表于 2025-5-11 12:27

假设检验时是使用左尾、右尾，还是双尾完全取决于你的对立假设，和概率大小无关。
对于同一个原假设，你也可以提出不同的对立假设，并因此决定是用哪种检验。最常见的例子就是均值检验时，对立假设如果为样本均值低于、高于或不等于总体均值，则相应使用左尾、右尾和双尾检验。
卡方检验有很多应用，但是大部分都是拿来检验两种分布是否一致（有一种卡方检验可以测试两个随机变量是否独立，基本的思路也是一致的）。在这样的实用场景下，你的对立假设基本上都是两种分布不同（卡方分布值大），所以使用时只看右尾。
但是在某些特殊场景下，也可能进行左尾，比较著名的例子是这篇论文：https://web.archive.org/web/20120426072009/http://www.amjbot.org/content/88/5/737.full。里面论述了孟德尔当年的豌豆实验结果分布和理论值过于接近，怀疑数据可能被捏造，这种情况下使用的卡方检验的对立假设为分布太过于一致，就得看左尾。

图文播报

[分享] 假设检验如何选择拒绝域?

登陆有奖并可浏览互动！

发表回复

浏览过的版块

官方推荐 /3

个人中心