登陆有奖并可浏览互动!
您需要 登录 才可以下载或查看,没有账号?立即注册


×
一、基础知识
1. 数据的种类
我们都知道,一般数据可以分为两类,即定性数据(类别型数据)和定量数据(数值型数据)
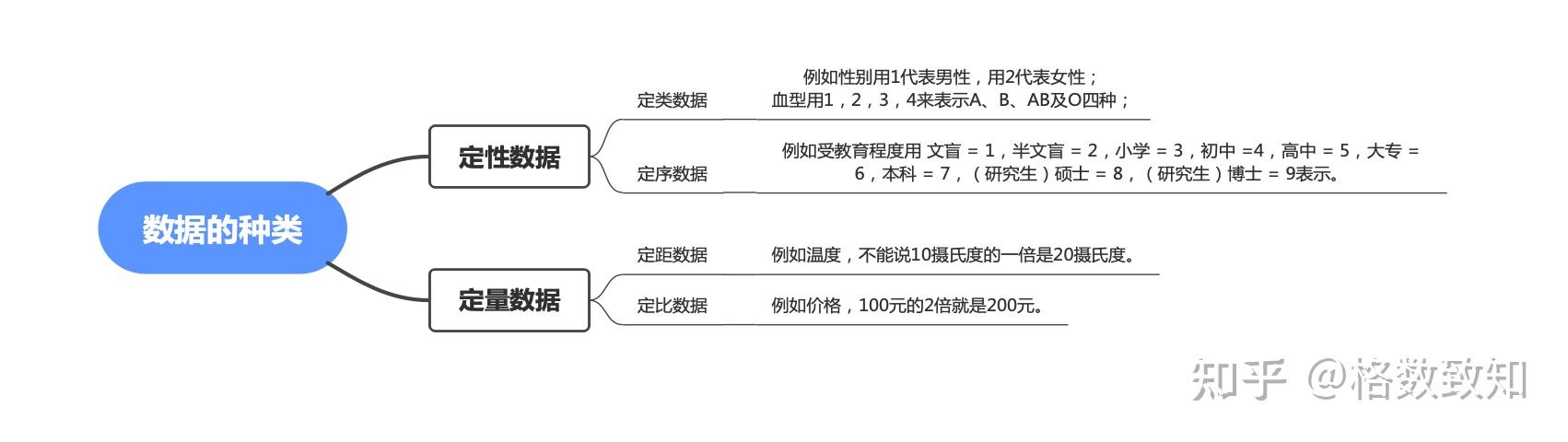
(1). 定性数据,表示研究对象的类别。很好理解,这里的表示类别用的数字既没有大小之分,也没有先后顺序之分,更不能进行算术四则运算。
定性数据可以分为:
① 定类数据
表现为类别,但不区分顺序,是由定类尺度计量形成的。一般可以从非数值型数据中编码转换而来,数值本身没有意义,只是为了区分类别做出的数值型标识
例如性别用1代表男性,用2代表女性;血型用1,2,3,4来表示A、B、AB及O四种;
② 定序数据
表现为类别,但有顺序,是由定序尺度计量形成的。运算符也没有意义,
例如受教育程度用 文盲 = 1,半文盲 = 2,小学 = 3,初中 =4,高中 = 5,大专 = 6,本科 = 7,(研究生)硕士 = 8,(研究生)博士 = 9表示。
(2). 定量数据,表示的是研究对象的数量特征,如人群中人的身高、体重等。
定量数据可以分为以下几种:
① 定距数据
表现为数值,可进行加、减运算,是由定距尺度计量形成的。定距数据的特征是没有绝对的零点,例如温度,不能说10摄氏度的一倍是20摄氏度。因此乘、除法对于定距数据来说也是没有意义的。
② 定比数据
表现为数值,可进行加、减、乘、除运算,是由定比尺度计量形成的。定比数据存在绝对的零点。例如价格,100元的2倍就是200元。
2. 描述性统计(略)
3. 数据分布(略)
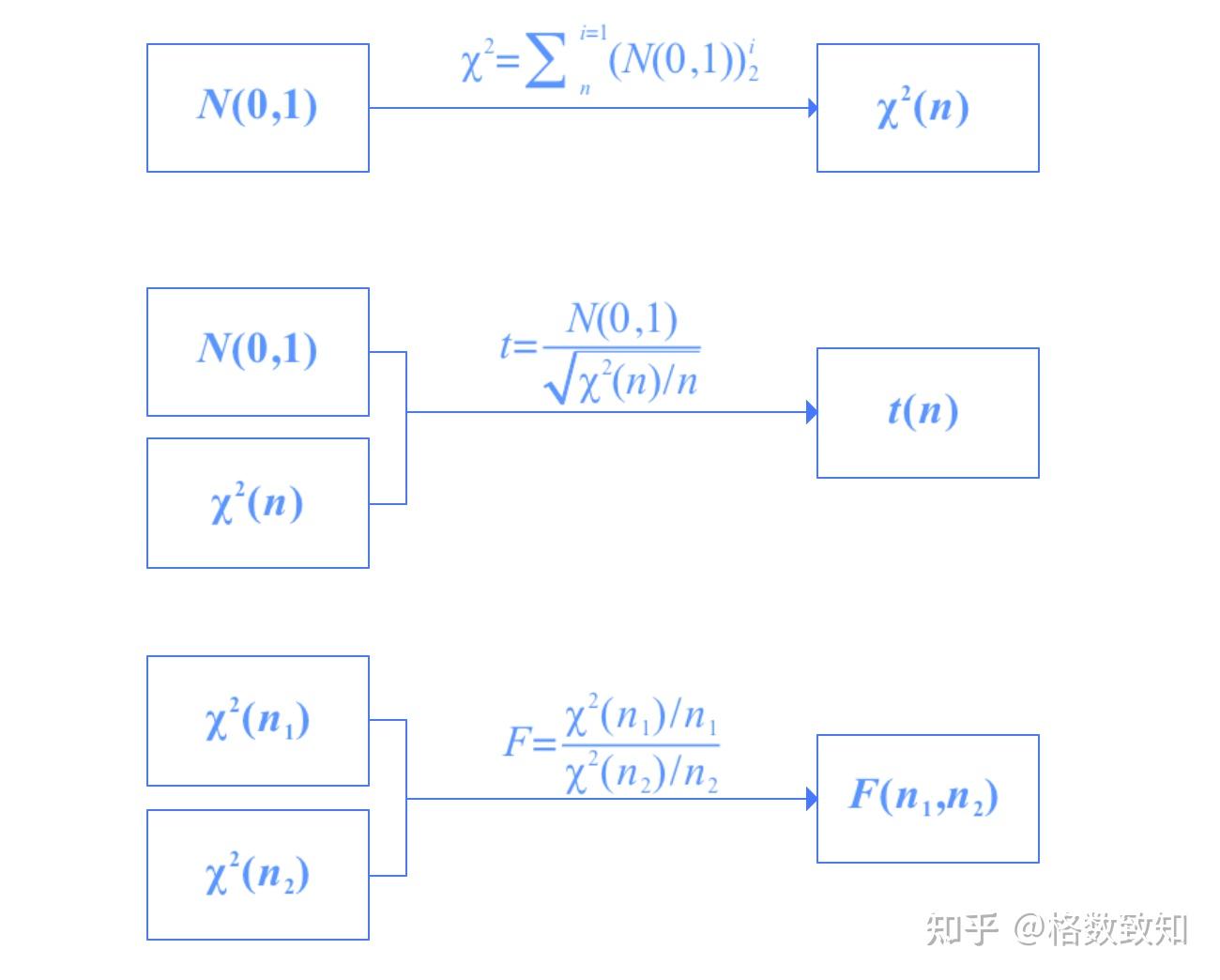
三大分布的转换
4. 区间估计(略)
注:篇幅所限,以上标了略的部分可以关注后私信我”统计学“获取完整版
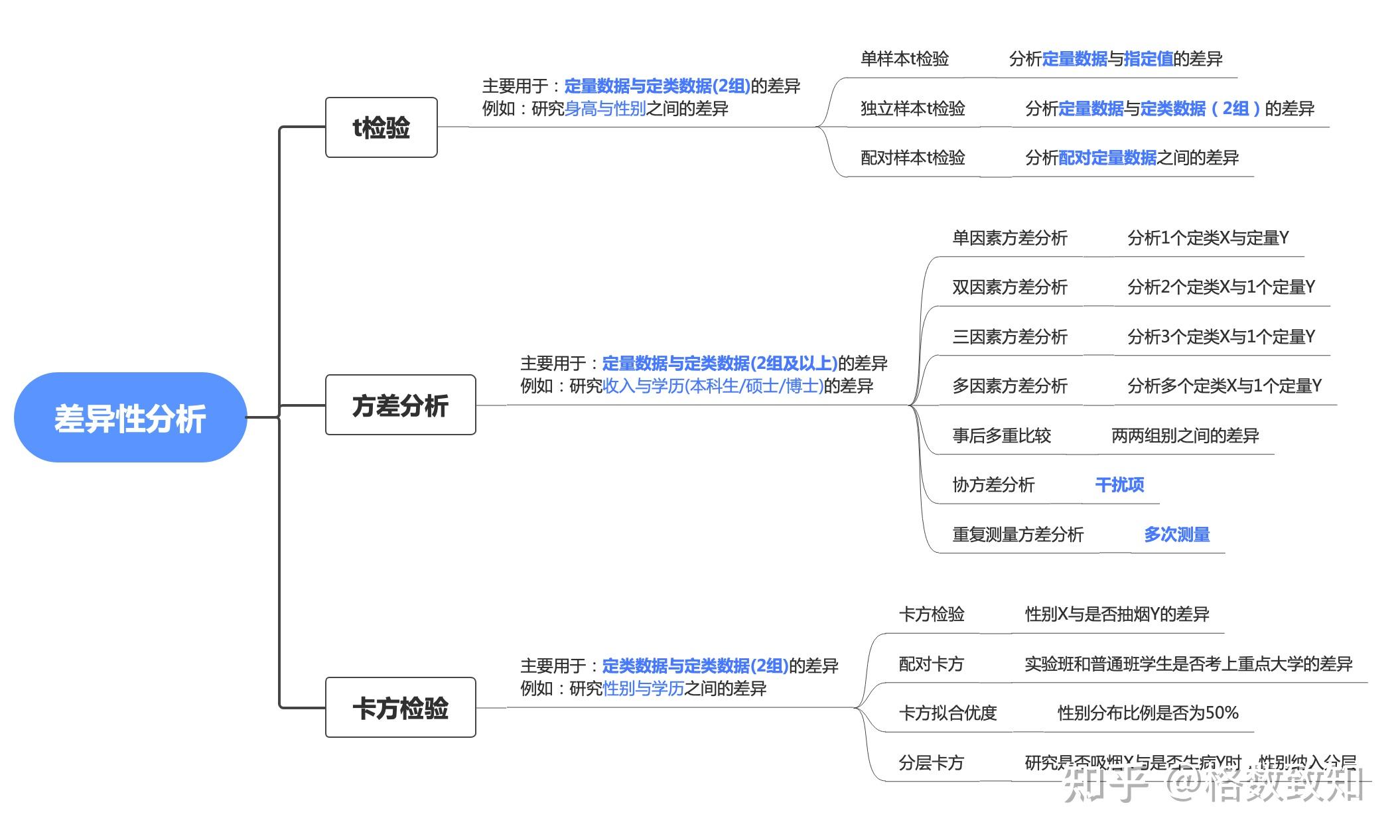
5. 假设检验
久经考场的你肯定对于很多概念类题目里问到的 “区别和联系” 不陌生,与之类似,在统计领域要研究的是数据之间的区别和联系 ,也就是差异性分析和相关性分析。本节我们重点关注数据的差异性分析。
我们知道,比较两个数之间的大小,要么前后两者求差,要么求比。差值大于零说明前者大于后者。比值大于1说明分子大于分母。
那么如何比较两组数据的差异性呢?大道至简,其实和上面原理类似
我们先从简单的看起,先比较一组数和一个给定数的差异,即,单个总体的差异性分析:
单个总体的假设检验
常见的单个总体差异性的假设检验分为3个类型:均值、比例、方差
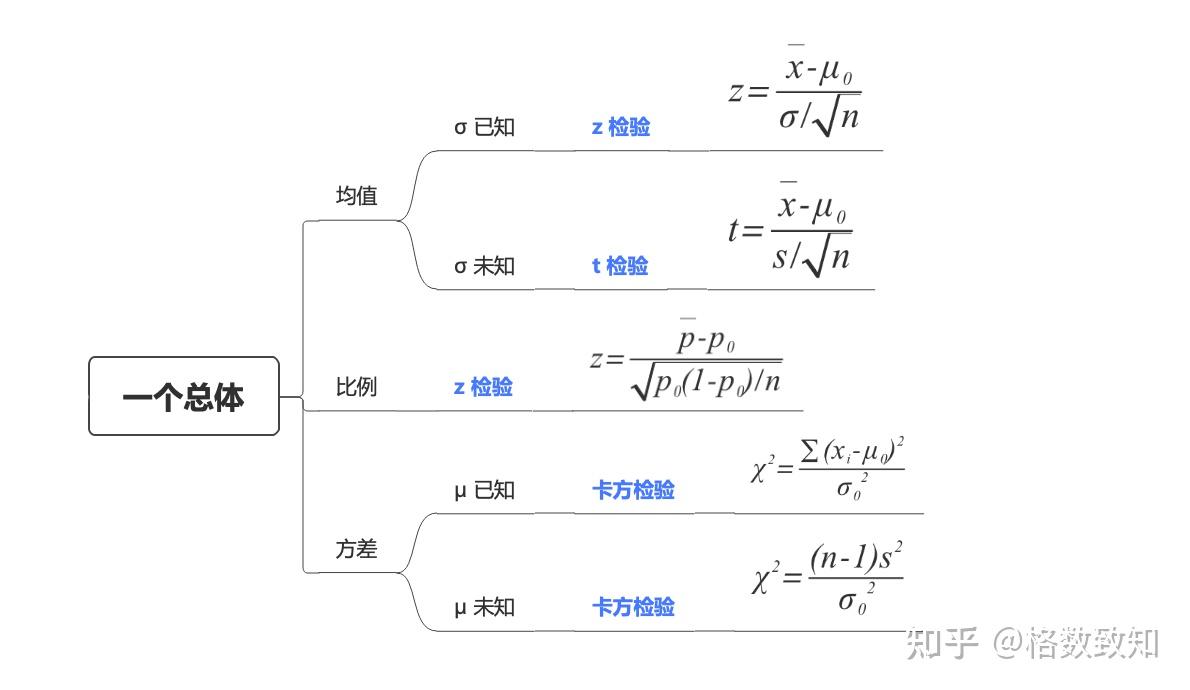
一个总体均值的假设检验 (指定值和样本均值)
顾名思义,就是检验指定值与样本均值的差异,按\sigma是否已知可以分2种情况:
① \sigma已知的情况: z 检验
接下来我们用代码举例实现一下你就明白怎么用了:
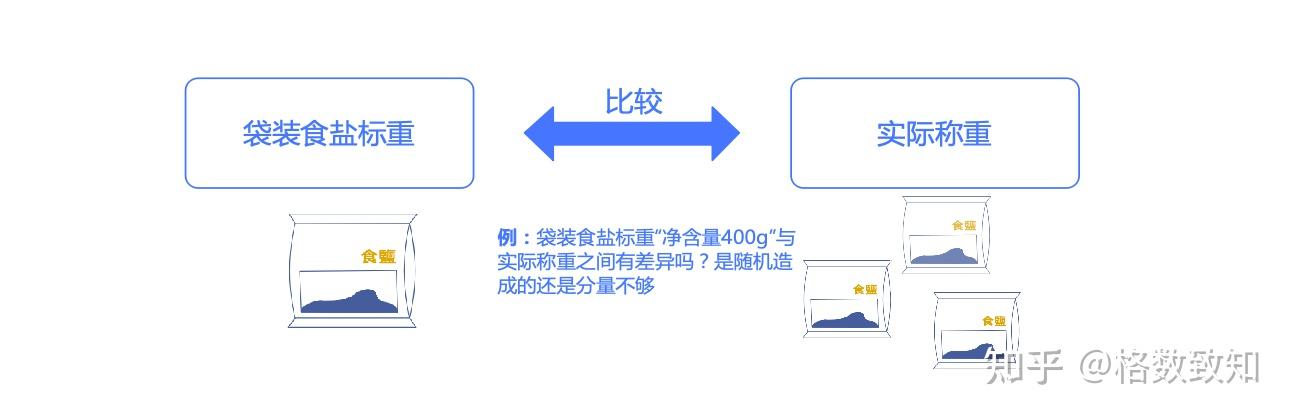
例5.1 检验一批厂家生产的红糖是否够标重
监督部门称了50包标重500g的红糖,均值是498.35g,少于所标的500g。对于厂家生产的这批红糖平均起来是否够份量,需要统计检验。
分析过程: 由于厂家声称每袋500g,因此原假设为总体均值等于500g(被怀疑对象总是放在零假设)。而且由于样本均值少于500g(这是怀疑的根据),把备择假设设定为总体均值少于500g (上面这种备选假设为单向不等式的检验称为单侧检验,而备选假设为不等号“≠”的称为双侧检验,后面会解释)
于是我们有了原假设和备择假设
H_0:\mu = 500 \leftrightarrow H_1:\mu <500:
引入相关库、读取数据如下
from scipy import stats
import scipy.stats
import numpy as np
import pandas as pd
import statsmodels.stats.weightstats
data = [493.01,498.83,494.16,500.39,497.63,499.72,493.41,498.97,501.94,503.45,497.47,494.19,500.99,495.81,499.63,494.91,498.90,502.43,491.34,497.50,505.95,496.56,501.66,492.02,497.68,493.48,505.40,499.21,505.84,499.41,505.65,500.51,489.53,496.55,492.26,498.91,496.65,496.38,497.16,498.91,490.98,499.97,501.21,502.85,494.35,502.96,506.21,497.66,504.66,492.11]
进行z检验:
z, pval = statsmodels.stats.weightstats.ztest(data, value=500,alternative = 'smaller')
# 'two-sided': 样本均值与给定的总体均值不同
# 'larger' : 样本均值小于给定总体均值
# 'smaller' : 样本均值大于给定总体均值
print(z,pval)
# -2.6961912076362085 0.0035068696715304876
结论: 选择显著性水平 0.05 的话,P=0.0035 < 0.05, 故应该拒绝原假设。具体来说就是该结果倾向于支持平均重量小于500g的备则假设。
② \sigma未知的情况: t 检验
例5.2 检验汽车实际排放是否低于其声称的排放标准
汽车厂商声称其发动机排放标准的一个指标平均低于20个单位。在抽查了10台发动机之后,得到下面的排放数据: 17.0 21.7 17.9 22.9 20.7 22.4 17.3 21.8 24.2 25.4 该样本均值为21.13.究竟能否由此认为该指标均值超过20?
分析过程: 由于厂家声称指标平均低于20个单位,因此原假设为总体均值等于20个单位(被怀疑对象总是放在零假设)。而且由于样本均值大于20(这是怀疑的根据),把备择假设设定为总体均值大于20个单位
于是我们有了原假设和备择假设
H_0:\mu = 20 \leftrightarrow H_1:\mu > 20:
读取数据如下
data = [17.0, 21.7, 17.9, 22.9, 20.7, 22.4, 17.3, 21.8, 24.2, 25.4]
进行t检验如下:
import scipy.stats
t, pval = scipy.stats.ttest_1samp(a = data, popmean=20,alternative = 'greater')
# 说明
# a 为给定的样本数据
# popmean 为给定的总体均值
# alternative 定义备择假设。以下选项可用(默认为“two-sided”):
# ‘two-sided’:样本均值与给定的总体均值(popmean)不同
# ‘less’:样本均值小于给定总体均值(popmean)
# ‘greater’:样本均值大于给定总体均值(popmean)
print(t, pval)
# '''
# P= 0.004793 < 5%, 拒绝原假设,接受备择假设样本
# '''
结论: 选择显著性水平 0.01 的话,P=0.1243 > 0.05, 故无法拒绝原假设。具体来说就是该结果无法支持指标均值超过20的备则假设。
一个总体比例的假设检验(指定比例和样本比例)
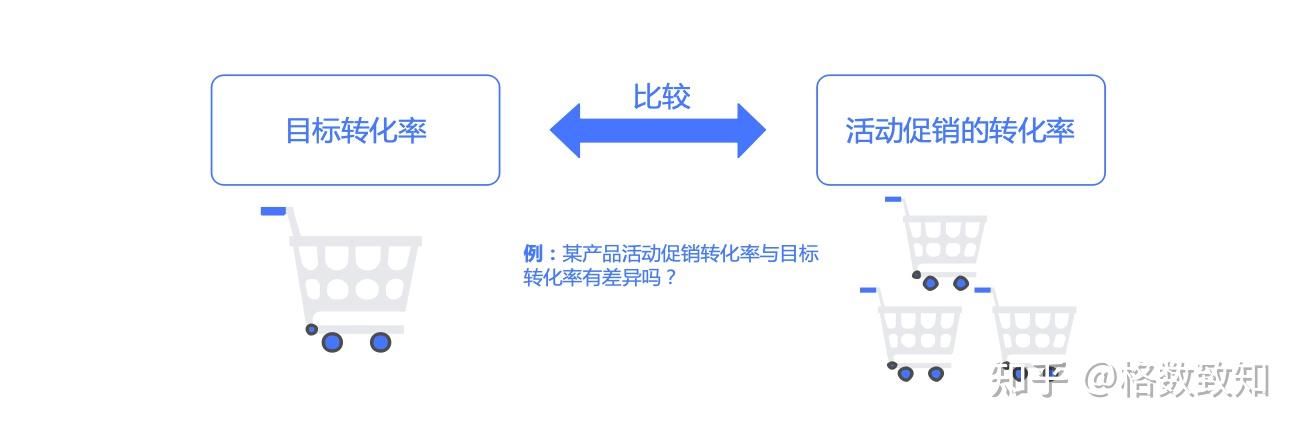
例5.3 检验高尔夫球场女性球员比例是否因促销活动而升高
某高尔夫球场去年打球 的人当中有20%是女性,为了增加女性球员的比例,该球场推出了一项促销活动来吸引更多的女性参加高尔夫运动,在活动实施了1个月后,球场的研究者想通过统计分析研究确定高尔夫球场的女性球员比例是否上升,收集到了400个随机样本,其中有100是女性
分析过程: 由于研究的是女性球员所占的比例是否上升,因此选择上侧检验比较合适,备择假设是比例大于20%
H_0:p \leqslant 0.20 \leftrightarrow H_1:p > 0.20:
方法1:用statsmodels.stats.proportion里面的proportions_ztest函数计算(推荐)
import numpy as np
from statsmodels.stats.proportion import proportions_ztest
count = 100
nobs = 400
p_0 = 0.2
p_bar = count/nobs
p_0 = 0.2
n = 400
# 执行单一样本比例检验 statsmodels.stats.proportion.proportions_ztest
z_statistic, p_value = proportions_ztest(count, nobs, value = p_0,alternative='larger',prop_var = value)
# 注:statsmodels.stats.proportion.proportions_ztest 的函数有几个问题:讲在第八节之后说明,感兴趣的读者请持续关注
# 打印结果
print("z统计量:", z_statistic)
print("p值:", p_value)
#z统计量: 2.4999999999999996
#p值: 0.006209665325776138
方法2 用手动方式计算
count = 100
nobs = 400
p_0 = 0.2
p_bar = count/nobs
p_0 = 0.2
n = 400
def calc_z_score(p_bar, p_0, n):
z = (p_bar - p_0) / (p_0 * (1 - p_0) / n)**0.5
return z
z = calc_z_score(p_bar, p_0, n)
p = stats.norm.sf(z)
# 打印结果
print("z统计量:", z)
print("p值:", p)
# z统计量: 2.4999999999999996
# p值: 0.006209665325776138
结论: 选择显著性水平 0.05 的话,P=0.0062 < 0.05, 拒绝原假设。具体来说就是该结果支持特定的促销活动能够提升该球场女性运动员比例的备则假设。
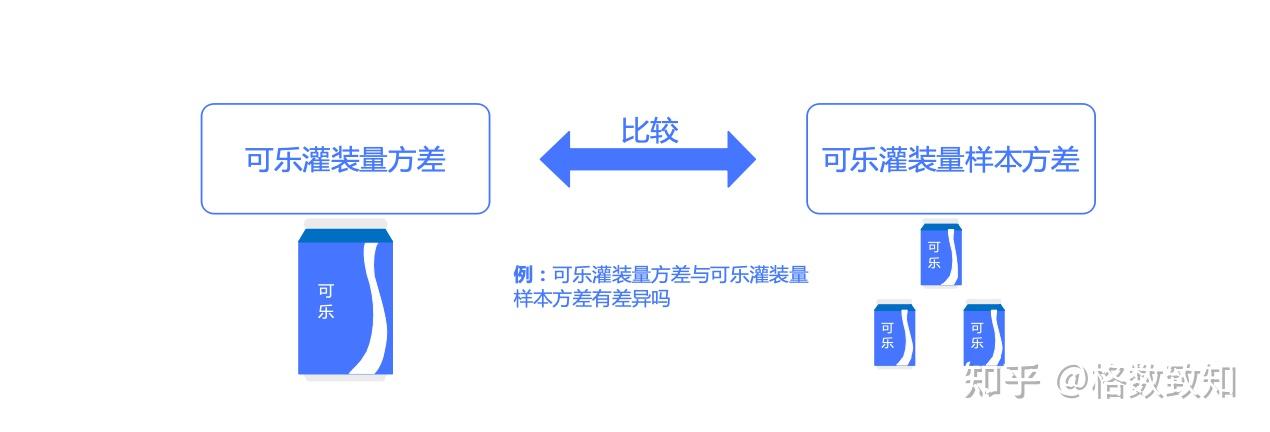
一个总体方差的假设检验(指定方差和样本方差)
import numpy as np
from scipy import stats
def chi2test(sample_var, sample_num,sigma_square,side, alpha=0.05):
'''
参数:
sample_var--样本方差
sample_num--样本容量
sigma_square--H0方差
返回值:
pval
'''
chi_square =((sample_num-1)*sample_var)/(sigma_square)
p_value = None
if side == 'two-sided':
p = stats.chi2(df=sample_num-1).cdf(chi_square)
p_value = 2*np.min([p, 1-p])
elif side == 'less':
p_value = stats.chi2(df=sample_num-1).cdf(chi_square)
elif side == 'greater':
p_value = stats.chi2(df=sample_num-1).sf(chi_square)
return chi_square,p_value
例5.4 检验公交车到站时间的方差是否比规定标准大
某市中心车站为规范化提升市民对于公交车到站时间的满意度,对于公交车的到站时间管理做了规定,标准是到站时间的方差不超过4。为了检验时间的到站时间的方差是否过大,随机抽取了24辆公交车的到站时间组成一个样本,得到的样本方差是 s^2=4.9,假设到站时间的总体分布符合正态分布,请分析总体方差是否过大。
分析过程: 由于研究的是方差是否过大,因此选择上侧检验比较合适,备择假设是方差大于4
于是我们有了原假设和备择假设
H_0: \sigma^2 \leqslant 4 \leftrightarrow H_1:\sigma^2 > 4:
chi_square,p_value = chi2test(sample_var = 4.9, sample_num = 24, sigma_square = 4,side='greater')
print("p值:", p_value)
# p值: 0.2092362676676498
结论: 选择显著性水平 0.05 的话,P=0.2092 > 0.05, 无法拒绝原假设。具体来说就是该结果不支持方差变大的备则假设。
例5.5 检验某考试中心升级题库后考生分数的方差是否有显著变化
某数据分析师认证考试机构CDA考试中心,历史上的持证人考试分数的方差为 \sigma^2=100,现在升级了题库,该考试中心希望新型考题的方差保持在原有水平上,为了研究该问题,收集到了30份新考题的考分组成的样本,样本方差是\sigma^2=152,在 \alpha=0.05的显著性水平下进行假设检验。
分析过程:由于目标是希望考试分数的方差保持原有水平,因此选择双侧检验
于是我们有了原假设和备择假设
H_0: \sigma^2 =100 \leftrightarrow H_1:\sigma^2 \neq 100:
p_value = chi2test(sample_var = 162, sample_num = 30, sigma_square = 100,side='two-sided')
print("p值:", p_value)
# p值: 0.07213100536907469
结论: 选择显著性水平 0.05 的话,P=0.0721 > 0.05, 故无法拒绝原假设。具体来说就是不支持方差发生了变化的备则假设。
两个总体的假设检验
常见的两总体差异性的假设检验也分3个类型:均值、比例、方差
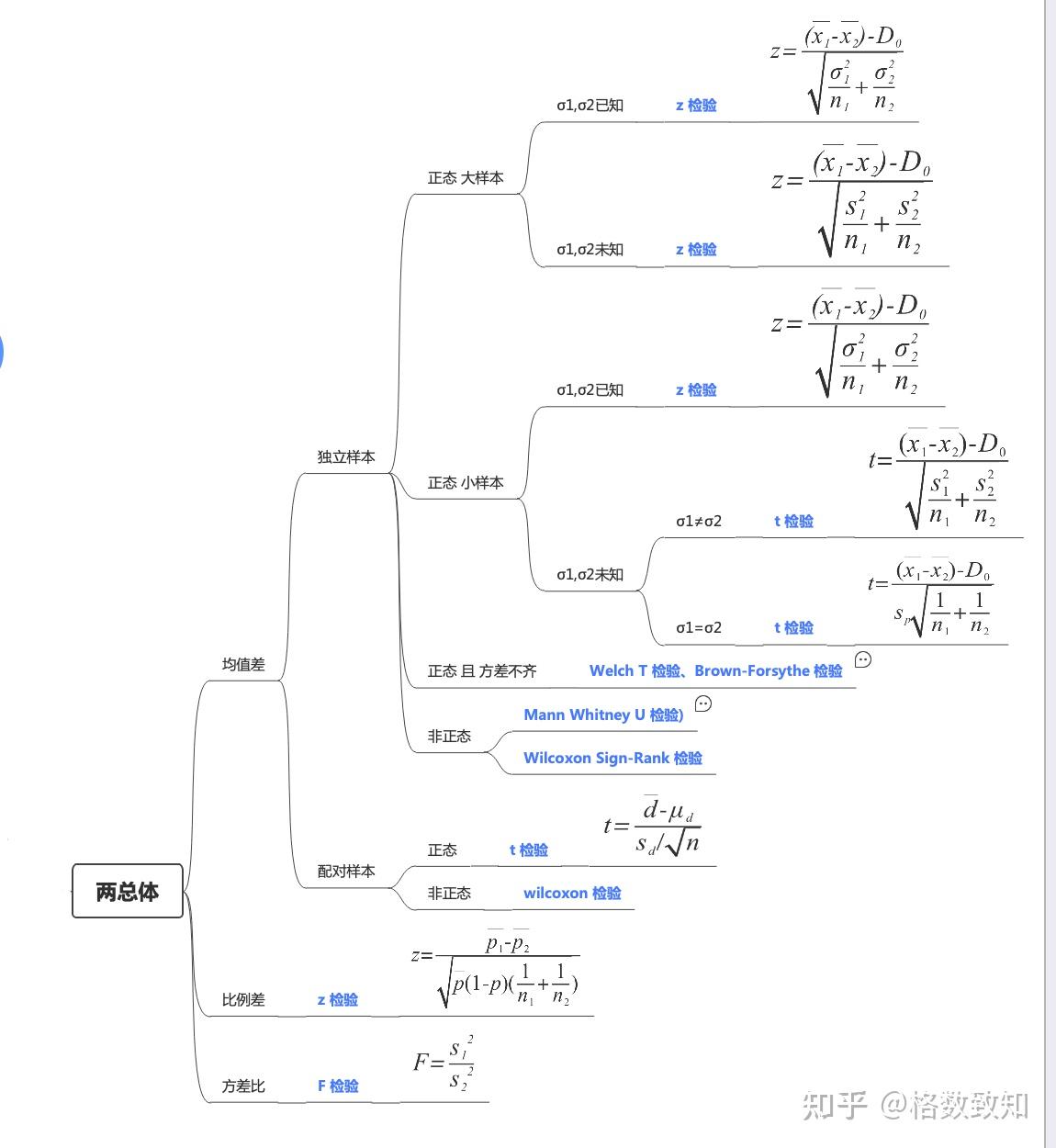
两总体均值之差的假设检验(独立样本)
例5.6(数据:drug.txt) 检验某药物在实验组的指标是否低于对照组
为检测某种药物对情绪的影响,对实验组的100名服药者和对照组的150名非服药者进行心理测试,得到相应的某指标。需要检验实验组指标的总体均值\mu_1是否大于对照组的指标的总体均值\mu_2。这里假定两个总体独立地服从正态分布。相应的假设检验问题为:
分析过程:由于目标是检验实验组指标的总体均值\mu_1是否大于对照组的指标的总体均值\mu_2,因此选择上侧检验
于是我们有了原假设和备择假设
H_0: \mu_1 \leqslant \mu_2 \leftrightarrow H_1:\mu_1 > \mu_2:
data = pd.read_table("./t-data/drug.txt",sep = ' ')
data.sample(5)
| ah | id | | 4.4 | 2 | | 6.8 | 2 | | 9.6 | 2 | | 4.8 | 2 | | 13.2 | 1 |
a = data[data['id']==1]['ah']
b = data[data['id']==2]['ah']
'''
H0: 实验组的均值等于对照组
H1: 实验组的均值大于对照组
'''
t, pval = scipy.stats.ttest_ind(a,b,alternative = 'greater')
print(t,pval)
# 0.9109168350628888 0.18161186154576608
结论: 选择显著性水平 0.05 的话,p = 0.1816 > 0.05,无法拒绝H0,具体来说就是该结果无法支持实验组均值大于对照组的备则假设。
两总体均值之差的假设检验(配对样本)
例5.7(数据: diet.txt) 检验减肥前后的重量是否有显著性差异(是否有减肥效果)
这里有两列50对减肥数据。其中一列数据(变量名before)是减肥前的重量,另一列(变量名after)是减肥后的重量(单位: 公斤),人们希望比较50个人在减肥前和减肥后的重量。
分析过程:这里不能用前面的独立样本均值差的检验,这是因为两个样本并不独立。每一个人减肥后的重量都和自己减肥前的重量有关,但不同人之间却是独立的,所以应该用配对样本检验。同时,由于研究的是减肥前后的重量变化,期望减肥前的重量大于减肥后的重量,所以备择假设是期望减肥前的重量大于减肥后的重量
于是我们有了原假设和备择假设:
H_0: \mu_1 = \mu_2 \leftrightarrow H_1:\mu_1 > \mu_2:
data = pd.read_table("./t-data/diet.txt",sep = ' ')
data.sample(5)
| before | after | | 58 | 50 | | 76 | 71 | | 69 | 65 | | 68 | 76 | | 81 | 75 |
a = data['before']
b = data['after']
stats.ttest_rel(a, b,alternative = 'greater')
# Ttest_relResult(statistic=3.3550474801424173, pvalue=0.000769424325484219)
结论 选择显著性水平 0.05 的话,p = 0.0007 < 0.05,故应该拒绝原假设。具体来说就是该结果倾向支持减肥前后的重量之差大于零(即减肥前重量大于减肥后,也就是有减肥效果)的备则假设。
两总体比例之差的假设检验
import numpy as np
import scipy.stats as stats
def proportion_test(p1, p2, n1, n2, side='two-sided'):
"""
参数:
p1: 样本1的比例
p2: 样本2的比例
n1: 样本1的数量
n2: 样本2的数量
side: 假设检验的方向,可选'two-sided'(双侧检验,默认), 'greater'(右侧检验), 'less'(左侧检验)
返回值:
z_value: Z统计量的值
p_value: 对应的p值
"""
p = (p1 * n1 + p2 * n2) / (n1 + n2)
se = np.sqrt(p * (1 - p) * (1 / n1 + 1 / n2))
z_value = (p1 - p2) / se
if side == 'two-sided':
p_value = 2 * (1 - stats.norm.cdf(np.abs(z_value)))
elif side == 'greater':
p_value = 1 - stats.norm.cdf(z_value)
elif side == 'less':
p_value = stats.norm.cdf(z_value)
else:
raise ValueError("Invalid side value. Must be 'two-sided', 'greater', or 'less'.")
return z_value, p_value
例5.8 检验不同保险客户的索赔率是否存在差异
某保险公司抽取了单身与已婚客户的样本,记录了他们在一段数据内的索赔次数,计算了索赔率,现在需要检验两种保险客户的索赔率是否存在差异
分析过程:由于目标比例是否有差异,因此选择比例之差的双侧检验
于是我们有了原假设和备择假设
H_0: p_1 = p_2 \leftrightarrow H_1:p_1 \neq p_2:
p1 = 0.14
p2 = 0.09
n1 = 250
n2 = 300
z_value, p_value = proportion_test(p1, p2, n1, n2, side='two-sided')
# 选择双侧检验 alternative = 'two-sided'
print("Z_value:", z_value)
print("p_value:", p_value)
# Z_value: 1.846189280616294
# p_value: 0.0648647268570739
结论 选择显著性水平 0.05 的话,p = 0.0648 > 0.05,故无法拒绝原假设。具体来说就是该结果无法支持两种保险客户的索赔率存在差异的备则假设。
两总体方差之比的假设检验
import numpy as np
from scipy import stats
def f_test_by_s_square(n1, n2, s1_square,s2_square, side ='two-sided'):
"""
参数
n1 :样本1的数量
n2 :样本2的数量
s1_square:样本1的方差
s2_square:样本2的方差
#
# F_value :F统计量的值
# p_value :对应的p值
"""
F_value = s1_square/s2_square
F = stats.f(dfn = n1-1, dfd = n2-1)
if side=='two-sided':
print("two-sided")
p_value = 2*min(F.cdf(F_value), 1-F.cdf(F_value))
return F_value,p_value
elif side=='greater':
print("greater")
p_value = 1-F.cdf(F_value)
return F_value,p_value
例5.9 检验不同公交公司的校车到达时间的方差是否有差异
某学校的校车合同到期,先需要在A、B两个校车供应公司中选择一个,才有到达时间的方差作为衡量服务质量的标准,较低方差说明服务质量稳定且水平较高,如果方差相等,则会选择价格更低的公司,,如果方差不等,则优先考虑方差更低的公司。 现收集到了A公司的26次到达时间组成一个样本,方差68,B公司16次到达时间组成一个样本,方差是30,请检验AB两个公司的到达时间方差。
分析过程:由于目标是希望的方差保持原有水平,因此选择双侧检验。两总体方差之比用F检验,将方差较大的A视为总体1
于是我们有了原假设和备择假设
H_0: \sigma_1 = \sigma_2 \leftrightarrow H_1: \sigma_1 \neq \sigma_2 :
f_statistic , p_value= f_test_by_s_square(n1=26, n2=16,s1_square=78,s2_square=20,side='two-sided')
# 选择双侧检验所以side='two-sided'
# 打印检验结果
print("F statistic:", f_statistic)
print("p-value:", p_value)
#two-sided
#F statistic: 3.9
#p-value: 0.00834904415829052
结论 选择显著性水平 0.05 的话,p = 0.0083 < 0.05,故拒绝原假设。结果倾向支持AB两个公司的到达时间方差存在差异的备则假设。
例5.10 检验修完Python课程的学生是否比修完数据库课程的学生考CDA的成绩方差更大
某高校数据科学专业的学生,修完一门数据库课程的41名学生考CDA的方差s^2=120,修完Python课程的31名学生考CDA的方差是s^2=80,这些数据是否表明,修完数据库的学生要比修完Python的学生CDA成绩的方差更大?
分析过程:由于目标是希望修完Python的学生CDA成绩的方差更大,因此选择上侧检验。两总体方差之比用F检验,将方差较大的数据库课程的考试成绩视为总体1
于是我们有了原假设和备择假设
H_0: \sigma_1 < \sigma_2 \leftrightarrow H_1: \sigma_1 \geqslant \sigma_2 :
f_statistic , p_value= f_test_by_s_square(n1=41, n2=31,s1_square=120,s2_square=80,side='greater')# 打印检验结果
# 选择上侧检验所以side='greater'
print("F statistic:", f_statistic)
print("p-value:", p_value)
结论 选择显著性水平 0.05 的话,p = 0.1256 > 0.05,故无法拒绝原假设。结果无法支持修完数据库的学生要比修完Python的学生CDA成绩的方差更大的备则假设。
关于知识的学习,你会发现有很多相似的逻辑,抓住问题的本质去理解的话就没那么复杂了,比如概念题里面的 区别和联系 延伸到数据分析里的差异性和相关性;再比如计算机数据结构里的 树、森林、网络 到机器学习里面的决策树、随机森林、神经网络;再比如从 互联网、区块链到元宇宙,都是想通过技术的手段去刻画客观世界;算法应用里面的图像识别、语音识别,替代人的眼耳鼻舌身意中的前二者去感知世界。抓住了问题的本质不仅可以帮助我们理解知识,还可以将一个领域的知识或模型迁移到另一个领域加以创新和应用。

假设检验背后的故事:统计学史上最著名的女士品茶
下期将为大家带来《统计学极简入门》之方差分析
关注后私信”统计学“获取本文.md代码文件
6. 方差分析
单因素多水平方差分析
例6.1 不同装配方式对生产的过滤系统数量的差异性检验
某城市过滤水系统生产公司,有A、B、C3种方式进行过滤水系统的装配,该公司为了研究三种装配方式生产的过滤系统数量是否有差异,从全体装配工人中抽取了15名工人,然后随机地指派一种装配方式,这样每个装配方式就有5个工人。在指派装配方法和培训工作都完成后,一周内对每名工人的装配过滤系统数量进行统计如下:
| 方法A | 方法B | 方法C | | 58 | 58 | 48 | | 64 | 69 | 57 | | 55 | 71 | 59 | | 66 | 64 | 47 | | 67 | 68 | 49 |
请根据数据判断3种装配方式有无差异
分析过程:由于目标是判断3种装配方式有无差异,多样本的检验用方差分析
于是我们有了原假设和备择假设
H_0: \mu_1 = \mu_2 = \mu_3 \leftrightarrow H_1:均值不全相等
import pandas as pd
import numpy as np
from scipy import stats
# 数据
A = [58,64,55,66,67]
B = [58,69,71,64,68]
C = [48,57,59,47,49]
data = [A, B, C]
# 方差的齐性检验
w, p = stats.levene(*data)
if p < 0.05:
print('方差齐性假设不成立')
# 成立之后, 就可以进行单因素方差分析
f_value, p_value = stats.f_oneway(*data)
# 输出结果
print("F_value:", f_value)
print("p_value:", p_value)
F_value: 9.176470588235295
p_value: 0.0038184120755124806
结论 选择显著性水平 0.05 的话,p = 0.0038 < 0.05,故拒绝原假设。支持三种装配方式装配数量均值不全相等的备则假设。
例6.2 不同优惠金额对购买转化率的差异性检验
某公司营销中心为了提升销量,针对某产品设计了3种不同金额的优惠,想测试三种优惠方式对于用户的购买转化率是否有显著影响,先收集到了三种不同方式在6个月内的转化率数据
请根据数据判断3种不同优惠金额的转化率有无差异
| 优惠A | 优惠B | 优惠C | | 0.043 | 0.05 | 0.048 | | 0.047 | 0.048 | 0.05 | | 0.051 | 0.045 | 0.047 | | 0.049 | 0.055 | 0.056 | | 0.045 | 0.048 | 0.054 | | 0.0469 | 0.0491 | 0.0509 |
分析过程:由于目标是判断3种不同金额的优惠券对于转化率有无差异,多样本的检验用方差分析
于是我们有了原假设和备择假设
H_0: \mu_1 = \mu_2 = \mu_3 \leftrightarrow H_1:认为这几组之间的购买率不一样
P < 0.05 拒绝原假设,倾向于支持不同优惠金额购买率不一样的备择假设。认为不同优惠金额会对购买率产生影响 P > 0.05 无法拒绝原假设。认为不同优惠金额不会对购买率产生影响
import pandas as pd
import numpy as np
from scipy import stats
A = [0.043 , 0.047 , 0.051 , 0.049 , 0.045 , 0.0469]
B = [0.05 , 0.048 , 0.045 , 0.055 , 0.048 , 0.0491]
C = [0.048 , 0.05 , 0.047 , 0.056 , 0.054 , 0.0509]
data = [A, B, C]
# 方差的齐性检验
w, p = stats.levene(*data)
if p < 0.05:
print('方差齐性假设不成立')
# 成立之后, 就可以进行单因素方差分析
f_value, p_value = stats.f_oneway(*data)
# 输出结果
print("F_value:", f_value)
print("p_value:", p_value)
# F_value: 2.332956563862427
# p_value: 0.13116820340181937
结论 选择显著性水平 0.05 的话,p = 0.1311 > 0.05,故无法拒绝原假设。认为不同优惠金额不会对购买率产生影响
双因素方差分析
1.双因素方差分析(等重复实验)
这里的等重复实验,意思就是针对每个组合做大于等于两次的实验,比如下方例子中表里A1和B1的组合里面有2个数字,即说明做了两次实验,如果是3个数字则说明3次实验,依次类推。
例6.3 不同燃料种类和推进器的火箭射程差异性检验
火箭的射程与燃料的种类和推进器的型号有关,现对四种不同的燃料与三种不同型号的推进器进行试验,每种组合各发射火箭两次,测得火箭的射程如表(以海里计)(设显著性水平为0.05)
| 燃料 | B1 | B2 | B3 | | A1 | 58.2 , 52.6 | 56.2 , 41.2 | 65.3 , 60.8 | | A2 | 49.1 , 42.8 | 54.1 , 50.5 | 51.6 , 48.4 | | A3 | 60.1 , 58.3 | 70.9 , 73.2 | 39.2 , 40.7 | | A4 | 75.8 , 71.5 | 58.2 , 51.0 | 48.7 , 41.0 |
import numpy as np
import pandas as pd
d = np.array([[58.2, 52.6, 56.2, 41.2, 65.3, 60.8],
[49.1, 42.8, 54.1, 50.5, 51.6, 48.4],
[60.1, 58.3, 70.9, 73.2, 39.2, 40.7],
[75.8, 71.5, 58.2, 51.0, 48.7,41.4]
])
data = pd.DataFrame(d)
data.index=pd.Index(['A1','A2','A3','A4'],name='燃料')
data.columns=pd.Index(['B1','B1','B2','B2','B3','B3'],name='推进器')
# pandas宽表转长表
data = data.reset_index().melt(id_vars =['燃料'])
data = data.rename(columns={'value':'射程'})
data.sample(5)
| 燃料 | 推进器 | 射程 | | A2 | B3 | 48.4 | | A3 | B2 | 73.2 | | A3 | B3 | 39.2 | | A4 | B1 | 71.5 | | A2 | B2 | 54.1 |
import statsmodels.api as sm
from statsmodels.formula.api import ols
# 进行双因素方差分析
model = ols('射程~C(燃料) + C(推进器)+C(燃料):C(推进器)', data =data).fit()
# 打印方差分析表
anova_table = sm.stats.anova_lm(model, typ=2)
anova_table
| sum_sq | df | F | PR(>F) | | C(燃料) | 261.675 | 3 | 4.41739 | 0.025969 | | C(推进器) | 370.981 | 2 | 9.3939 | 0.00350603 | | C(燃料):C(推进器) | 1768.69 | 6 | 14.9288 | 6.15115e-05 | | Residual | 236.95 | 12 | nan | nan |
结论:
对燃料因素来说,其p = 0.0259 < 0.05 所以拒绝H_{01},认为燃料对射程影响显著;
对推进器因素来说,其p = 0.0035 < 0.05,所以拒绝H_{02},认为推进器对射程影响显著;
对燃料和推进器的交互因素来说,其p = 0.000062< 0.05 ,所以拒绝H_{03},认为交互因素其对射程影响显著。
2.双因素方差分析(无重复实验)
在等重复实验中,我们为了检验实验中两个因素的交互作用,针对每对组合至少要做2次以上实验,才能够将交互作用与误差分离开来,在处理实际问题时候,如果我们一直不存在交互作用,或者交互作用对实验指标影响极小,则可以不考虑交互作用,此时每对组合只做一次实验,类似下方例子中的表中数据:
例6.3 不同时间、不同地点颗粒状物含量差异性检验 无重复实验
下面给出了在5个不同地点、不同时间空气中的颗粒状物(单位:mg/m°)含 量的数据记录于表中,试在显著性水平\alpha = 0.05下检验不同时间、不同地点颗粒状物含量有无显著差异?(假设两者没有交互作用〉
| 因素B -地点 | | 因素A - 时间 | | 1995年10月 | 76 | 67 | 81 | 56 | 51 | | 1996年01月 | 82 | 69 | 96 | 59 | 70 | | 1996年05月 | 68 | 59 | 67 | 54 | 42 | | 1996年08月 | 63 | 56 | 64 | 58 | 37 |
import numpy as np
import pandas as pd
d = np.array([
[76,67,81,56,51],
[82,69,96,59,70],
[68,59,67,54,42],
[63,56,64,58,37]])
data = pd.DataFrame(d)
data.index=pd.Index(['1995年10月','1996年01月','1996年05月','1996年08月'],name='时间')
data.columns=pd.Index(['B1','B2','B3','B4','B5'],name='地点')
# pandas宽表转长表
data = data.reset_index().melt(id_vars =['时间'])
data = data.rename(columns={'value':'颗粒状物含量'})
data.sample(5)
随机查看5条转化后的数据:
| 时间 | 地点 | 颗粒状物含量 | | 1996年05月 | B4 | 54 | | 1995年10月 | B4 | 56 | | 1996年05月 | B3 | 67 | | 1996年01月 | B2 | 69 | | 1996年01月 | B3 | 96 |
import statsmodels.api as sm
from statsmodels.formula.api import ols
# 进行双因素方差分析
model = ols('颗粒状物含量~C(时间) + C(地点)', data =data).fit()
# 打印方差分析表
anova_table = sm.stats.anova_lm(model, typ=2)
anova_table
| sum_sq | df | F | PR(>F) | | C(时间) | 1182.95 | 3 | 10.7224 | 0.00103293 | | C(地点) | 1947.5 | 4 | 13.2393 | 0.000234184 | | Residual | 441.3 | 12 | nan | nan |
结论:
对时间因素来说,其p = 0.001033 < 0.05 所以拒绝H_{01},认为时间对颗粒状物含量影响显著;
对地点因素来说,其p = 0.000234 < 0.05,所以拒绝H_{02},认为地点对颗粒状物含量影响显著;

致敬:数理统计的大半江山的创造者——费希尔
关注后私信”统计学“获取本文.md代码文件
7. 相关性分析
前面的假设检验、方差分析基本上都是围绕差异性分析,不论是单个总体还是两个总体及以上,总之都是属于研究“区别”,从本节开始,我们关注“联系”,变量之间的关系分为 函数关系和相关关系。 本节这里重点探讨的是不同类型变量之间的相关性,千万记住一点相关性不代表因果性。除表中列出的常用方法外,还有Tetrachoric、\phi相关系数等。
| 变量类型 | 变量类型 | 相关系数计算方法 | 示例 | | 连续型变量 | 连续型变量 | Pearson(正态)/Spearman(非正态) | 商品曝光量和购买转化率 | | 二分类变量(无序) | 连续型变量 | Point-biserial | 性别和疾病指数 | | 无序分类变量 | 连续型变量 | 方差分析 | 不同教育水平的考试成绩 | | 有序分类变量 | 连续型变量 | 连续指标离散化后当做有序分类 | 商品评分与购买转化率 | | 二分类变量 | 二分类变量 | 数学公式: \chi^2 检验 联合 Cramer's V | 性别和是否吸烟 | | 二分类变量(有序) | 连续型变量 | Biserial | 乐器练习时间与考级是否通过 | | 无序分类变量 | 无序分类变量 | 数学公式: \chi^2 检验 / Fisher检验 | 手机品牌和年龄段 | | 有序分类变量 | 无序分类变量 | 数学公式: \chi^2 检验 | 满意度和手机品牌 | | 有序分类变量 | 有序分类变量 | Spearman /Kendall Tau相关系数 | 用户等级和活跃程度等级 |
连续型变量 vs 连续型变量 : Pearson / Spearmanr
Pearson
Pearson相关系数度量了两个连续变量之间的线性相关程度;
import random
import numpy as np
import pandas as pd
np.random.seed(10)
df = pd.DataFrame({'商品曝光量':[1233,1333,1330,1323,1323,1142,1231,1312,1233,1123],
'购买转化率':[0.033,0.034,0.035,0.033,0.034,0.029,0.032,0.034,0.033,0.031]})
df
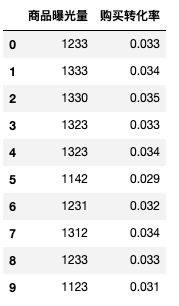
pd.Series.corr(df['商品曝光量'], df['购买转化率'],method = 'pearson') # pearson相关系数
# 0.885789300493948
import scipy.stats as stats
# 假设有两个变量X和Y
X = df['商品曝光量']
Y = df['购买转化率']
# 使用spearmanr函数计算斯皮尔曼相关系数和p值
corr, p_value = stats.pearsonr(X, Y)
print("Pearson相关系数:", corr)
print("p值:", p_value)
# Pearson相关系数: 0.8857893004939478
# p值: 0.0006471519603654732
Spearman等级相关系数
Spearman等级相关系数可以衡量非线性关系变量间的相关系数,是一种非参数的统计方法,可以用于定序变量或不满足正态分布假设的等间隔数据;
import random
import numpy as np
import pandas as pd
np.random.seed(10)
df = pd.DataFrame({'品牌知名度排位':[9,4,3,6,5,8,1,7,10,2],
'售后服务质量评价排位':[8,2,5,4,7,9,1,6,10,3]})
df
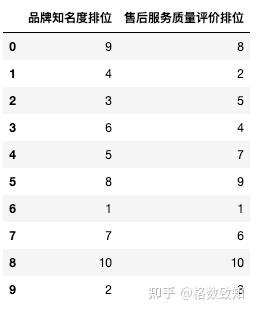
pd.Series.corr(df['品牌知名度排位'], df['售后服务质量评价排位'],method = 'spearman') # spearman秩相关
# 0.8787878787878788
import scipy.stats as stats
# 假设有两个变量X和Y
X = df['品牌知名度排位']
Y = df['售后服务质量评价排位']
# 使用spearmanr函数计算斯皮尔曼相关系数和p值
corr, p_value = stats.spearmanr(X, Y)
print("斯皮尔曼相关系数:", corr)
print("p值:", p_value)
# 斯皮尔曼相关系数: 0.8787878787878788
# p值: 0.0008138621117322101
结论:p = 0.0008<0.05,表明两变量之间的正向关系很显著。
二分类变量(自然)vs 连续型变量 :Point-biserial
假设我们想要研究性别对于某种疾病是否存在影响。我们有一个二元变量“性别”(男、女)和一个连续型变量“疾病指数”。我们想要计算性别与疾病指数之间的相关系数,就需要用到Point-biserial相关系数。
import scipy.stats as stats
# 创建一个列表来存储数据
gender = [0, 1, 0, 1, 1, 0]
disease_index = [3.2, 4.5, 2.8, 4.0, 3.9, 3.1]
# 使用pointbiserialr函数计算Point-biserial相关系数和p值
corr, p_value = stats.pointbiserialr(gender, disease_index)
print("Point-biserial相关系数:", corr)
print("p值:", p_value)
# Point-biserial相关系数: 0.9278305692406299
# p值: 0.007624695507848026
结论:p = 0.007<0.05,表明两变量之间的正向关系很显著。即性别与疾病指数正相关
无序分类变量 vs 连续型变量 : ANOVA
假设我们想要比较不同教育水平的学生在CDA考试成绩上是否存在显著差异。我们有一个无序分类变量“教育水平”(高中、本科、研究生)和一个连续型变量“考试成绩”。
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols
# 创建一个DataFrame来存储数据
data = pd.DataFrame({
'教育水平': ['高中', '本科', '本科', '研究生', '高中', '本科', '研究生'],
'考试成绩': [80, 90, 85, 95, 75, 88, 92]
})
# 使用ols函数创建一个线性模型
model = ols('考试成绩 ~ C(教育水平)', data=data).fit()
# 使用anova_lm函数进行方差分析
anova_table = sm.stats.anova_lm(model, typ=2)
anova_table
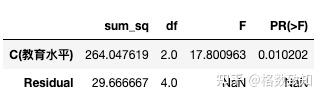
结论:p = 0.0102<0.05,拒绝原假设,表明两变量之间的正向关系很显著。教育水平与考试成绩正相关
有序分类变量 vs 连续型变量
将连续型变量离散化后当做有序分类,然后用 有序分类变量 VS 有序分类变量的方法
二分类变量 vs 二分类变量 : \chi^2 检验 联合 Cramer's V
一项研究调查了不同性别的成年人对在公众场合吸烟的态度,结果如表所示。那么,性别与对待吸烟的态度之间的相关程度
import numpy as np
from scipy.stats import chi2_contingency
observed = np.array([[15, 10],
[10, 26]])
observed
chi2, p, dof, expected = chi2_contingency(observed,correction =False) # correction =False
# 卡方值
# P值
# 自由度:
# 与原数据数组同维度的对应期望值
chi2, p
#(6.3334567901234555, 0.011848116168529757)
结论:p = 0.0118<0.05,拒绝原假设,表明两变量之间的正向关系很显著。
phi = np.sqrt(chi2/n)
print("phi's V:", phi)
# phi's V: 0.3222222222222222
卡方检验时有多种指标可表示效应量,可结合数据类型及交叉表格类型综合选择
- 第一:如果是2*2表格,建议使用 \phi指标
- 第二:如果是33,或 44表格,建议使用列联系数;
- 第三:如果是n*n(n>4)表格,建议使用 校正列联系数;
- 第四:如果是m*n(m不等于n)表格,建议使用 Cramer V指标;
- 第五:如果X或Y中有定序数据,建议使用 \lambda指标;
这里只列出 \phi指标 和 Cramer V指标 的计算,其他计算方式请读者自行研究。
# 计算Cramer's V
contingency_table = observed
n = contingency_table.sum().sum()
phi_corr = np.sqrt(chi2 / (n * min(contingency_table.shape) - 1))
v = phi_corr / np.sqrt(min(contingency_table.shape) - 1)
print("Cramer's V:", v)
# Cramer's V: 0.22878509151645754
二分类变量(有序) 连续型变量: Biserial
import numpy as np
from scipy.stats import pearsonr
# 生成随机的二元变量
binary_variable = np.random.choice([0, 1], size=100)
# 生成随机的连续变量
continuous_variable = np.random.normal(loc=0, scale=1, size=100)
# 注:此处的代码未经严格考证,请谨慎使用
def biserial_correlation(binary_variable, continuous_variable):
binary_variable_bool = binary_variable.astype(bool)
binary_mean = np.mean(binary_variable_bool)
binary_std = np.std(binary_variable_bool)
binary_variable_norm = (binary_variable_bool - binary_mean) / binary_std
corr, _ = pearsonr(binary_variable_norm, continuous_variable)
biserial_corr = corr * (np.std(continuous_variable) / binary_std)
return biserial_corr
# 计算Biserial相关系数
biserial_corr = biserial_correlation(binary_variable, continuous_variable)
print("Biserial相关系数:", biserial_corr)
Biserial相关系数: -0.2061772328681707
无序分类变量 vs 无序分类变量
参考 \chi^2 检验
有序分类变量 vs 无序分类变量
参考 \chi^2 检验
有序分类变量 vs 有序分类变量
Kendall秩相关系数
Kendall秩相关系数也是一种非参数的等级相关度量,类似于Spearman等级相关系数。
import random
import numpy as np
import pandas as pd
np.random.seed(10)
df = pd.DataFrame({'品牌知名度排位':[9,4,3,6,5,8,1,7,10,2],
'售后服务质量评价排位':[8,2,5,4,7,9,1,6,10,3]})
df
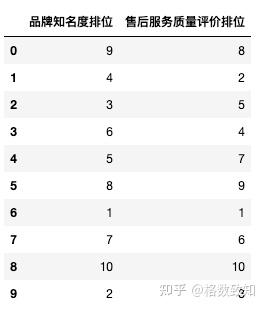
pd.Series.corr(df['品牌知名度排位'], df['售后服务质量评价排位'],method = 'kendall') # Kendall Tau相关系数
# 0.7333333333333333
from scipy.stats import kendalltau
# 两个样本数据
x = df['品牌知名度排位']
y = df['售后服务质量评价排位']
# 计算Kendall Tau相关系数
correlation, p_value = kendalltau(x, y)
print("Kendall Tau相关系数:", correlation)
print("p值:", p_value)
# Kendall Tau相关系数: 0.7333333333333333
# p值: 0.002212852733686067
浮生皆纵,恍如一梦,让我们只争朝夕,不负韶华! 二、案例分析
8. 再看t检验、F检验、\chi^2检验
前面在假设检验的部分经学过t检验、F检验、\chi^2检验,之所以再看,是想通过纵向对比这几个检验统计量以加深理解:
t检验
针对不同的场景,主要分为单样本T检验、独立样本T检验、配对样本T检验:
单样本的t检验
主要用于分析 一组定量数据 与 指定值的差异,例如检验食盐的实际称重是否不够标重的份量。

单样本T检验需要满足正态分布的假设,若不满足可采用单样本Wilcoxon检验。
例5.2 检验汽车实际排放是否低于其声称的排放标准
汽车厂商声称其发动机排放标准的一个指标平均低于20个单位。在抽查了10台发动机之后,得到下面的排放数据: 17.0 21.7 17.9 22.9 20.7 22.4 17.3 21.8 24.2 25.4 该样本均值为21.13.究竟能否由此认为该指标均值超过20?
分析过程: 由于厂家声称指标平均低于20个单位,因此原假设为总体均值等于20个单位(被怀疑对象总是放在零假设)。而且由于样本均值大于20(这是怀疑的根据),把备择假设设定为总体均值大于20个单位
于是我们有了原假设和备择假设
H_0:\mu = 20 \leftrightarrow H_1:\mu > 20:
读取数据如下
data = [17.0, 21.7, 17.9, 22.9, 20.7, 22.4, 17.3, 21.8, 24.2, 25.4]
分步骤计算过程如下:
步骤一:计算样本均值 \bar{X}=\frac{1}{n}\sum_{i=1}^nX_i =(17+21.7+...+25.4)/10=21.13
用Python:
x_bar = np.array(data).mean()
x_bar
# 21.13
步骤二:计算样本标准差
S = \sqrt{\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^2}
用Python计算:
s = np.sqrt(((data-x_bar)**2).sum()/len(data))
s
# 2.7481084403640255
步骤三:计算统计量
t = \frac{{\bar{X} - \mu}}{{\frac{{S}}{{\sqrt{n}}}}} ,其中 \mu 为整体均值20,自由度n-1为9
t = (x_bar - 20)/(s/np.sqrt(len(data)-1))
t
# 1.2335757753252794
步骤四:查表或用软件查询p值与
p_value = scipy.stats.t.sf(t,len(data)-1 )
p_value
# 0.1243024777589817
结论: 选择显著性水平 0.01 的话,P=0.1243 > 0.05, 故无法拒绝原假设。具体来说就是该结果无法支持指标均值超过20的备则假设。说明发动机排放指标是不合格的。
对于以上过程,我们也可以用scipy.stats.ttest_1samp函数,一步到位进行t检验,直接返回的就是t统计量和p值:
import scipy.stats
t, pval = scipy.stats.ttest_1samp(a = data, popmean=20,alternative = 'greater')
# 说明
# 单一样本的t检验,检验单一样本是否与给定的均值popmean差异显著的函数,第一个参数为给定的样本,第二个函数为给定的均值popmean,可以以列表的形式传输多个单一样本和均值。
# a 为给定的样本数据
# popmean 为给定的总体均值
# alternative 定义备择假设。以下选项可用(默认为“two-sided”):
# ‘two-sided’:样本均值与给定的总体均值(popmean)不同
# ‘less’:样本均值小于给定总体均值(popmean)
# ‘greater’:样本均值大于给定总体均值(popmean)
print(t, pval)
# '''
# P= 0.004793 < 5%, 拒绝原假设,接受备择假设样本
# '''
结论: 选择显著性水平 0.01 的话,P=0.1243 > 0.05, 故无法拒绝原假设。具体来说就是该结果无法支持指标均值超过20的备则假设。
独立样本的t检验
主要用于分析定量数据和定类数据(2组)的差异。原理是推论差异发生的概率,从而比较两个平均数的差异是否显著。通俗的说就是用样本均数和已知总体均数进行比较,来观察此组样本与总体的差异性。
例如有一个班的学生身高数据,如果学生的身高服从正态分布,想要研究身高和性别的关系,这个时候就相当于是两个独立样本。
独立样本的T检验也需要满足正态分布的假设,如果不满足可采用 Wilcoxon检验(也称MannWhitney检验); 如果满足但方差不等可采用 Welch T检验
计算公式如下:
t = \frac{{ (\bar{X}_1 - \bar{X}_2)-(\mu_1 - \mu_2)}} {{\sqrt{S_p^2 *(\frac{{1}}{{n_1}} + \frac{{1}}{{n_2}})}}}
\bar{X_{1}} 、 \bar{X_{2}} 代表两组数据的均值,
n_{1} 、 n_{2} 代表样本数,
S_p^2=\frac{{(n_1-1)S_1^2 +(n_2-1)S_2^2}}{{(n_1-1) - (n_2-1)}}
S_{1}^{2} 、 S_{2}^{2} 代表两组数组的方差。
从计算公式能看出来,t越小则两组数据差异性越小。具体多小就根据置信度和自由度查表对比理论统计量的大小得出两组数据差异性是否显著。
例5.6(数据:drug.txt) 检验某药物在实验组的指标是否低于对照组
为检测某种药物对情绪的影响,对实验组的100名服药者和对照组的150名非服药者进行心理测试,得到相应的某指标。需要检验实验组指标的总体均值\mu_1是否大于对照组的指标的总体均值\mu_2。这里假定两个总体独立地服从正态分布。相应的假设检验问题为:
分析过程:由于目标是检验实验组指标的总体均值\mu_1是否大于对照组的指标的总体均值\mu_2,因此选择上侧检验
于是我们有了原假设和备择假设
H_0: \mu_1 \leqslant \mu_2 \leftrightarrow H_1:\mu_1 > \mu_2:
data = pd.read_table("./t-data/drug.txt",sep = ' ')
data.sample(5)
| ah | id | | 4.4 | 2 | | 6.8 | 2 | | 9.6 | 2 | | 4.8 | 2 | | 13.2 | 1 |
a = data[data['id']==1]['ah']
b = data[data['id']==2]['ah']
'''
H0: 实验组的均值等于对照组
H1: 实验组的均值大于对照组
'''
t, pval = scipy.stats.ttest_ind(a,b,alternative = 'greater')
# 独立样本的T检验,检验两个样本的均值差异,该检验方法假定了样本的通过了F检验,即两个独立样本的方差相同
# 另一个方法是:
# stats.ttest_ind_from_stats(mean1, std1, nobs1, mean2, std2, nobs2, equal_var=True)
# 检验两个样本的均值差异(同上),输出的参数两个样本的统计量,包括均值,标准差,和样本大小:直接输入样本的描述统计量(均值,标准差,样本数)即可
print(t,pval)
# 0.9109168350628888 0.18161186154576608
结论: 选择显著性水平 0.05 的话,p = 0.1816 > 0.05,无法拒绝H0,具体来说就是该结果无法支持实验组均值大于对照组的备则假设。
配对样本t检验
主要用于分析配对定量数据的差异。
常见的使用场景有:
①同一对象处理前后的对比(同一组人员采用同一种减肥方法前后的效果对比);
②同一对象采用两种方法检验的结果的对比(同一组人员分别服用两种减肥药后的效果对比);
③配对的两个对象分别接受两种处理后的结果对比(两组人员,按照体重进行配对,服用不同的减肥药,对比服药后的两组人员的体重)。
例如,假设一个班上男女生的成绩不存在差异,显著性水平为0.05,可理解为只有5%的概率会出现“男女生成绩差异显著”的情况,若计算出的检验p值若小于0.05,则可以拒绝原假设。反之不能拒绝原假设。
此外,t检验注意事项
①无论哪种t检验、都要数据服从正态或者近似正态分布。正态性的检验方法有:正态图、正态性检验、P-P图/Q-Q图等。
②两个独立样本的t检验,通常需要先进行F检验(方差齐次检验),检验两个独立样本的方差是否相同,若两总体方差相等,则直接用t检验,若不等,可采用t’检验或变量变换或秩和检验等方法。
例5.7(数据: diet.txt) 检验减肥前后的重量是否有显著性差异(是否有减肥效果)
这里有两列50对减肥数据。其中一列数据(变量名before)是减肥前的重量,另一列(变量名after)是减肥后的重量(单位: 公斤),人们希望比较50个人在减肥前和减肥后的重量。
分析过程:这里不能用前面的独立样本均值差的检验,这是因为两个样本并不独立。每一个人减肥后的重量都和自己减肥前的重量有关,但不同人之间却是独立的,所以应该用配对样本检验。同时,由于研究的是减肥前后的重量变化,期望减肥前的重量大于减肥后的重量,所以备择假设是期望减肥前的重量大于减肥后的重量
于是我们有了原假设和备择假设:
H_0: \mu_1 = \mu_2 \leftrightarrow H_1:\mu_1 > \mu_2:
步骤一、计算两组样本数据差值d,即58-50,76-71,69-65,68-76,81-75
d = data['before'] - data['after']
步骤二、计算差值d的平均值 \bar{d} ,即(-1+0+1+0)/4=0
d_bar = ( d).sum()/len(data)
步骤三、计算差值d的标准差 S_d ,计算公式为
s_d = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (d_i - \bar{d})^2}
s_d = np.sqrt(((d -d_bar)**2).sum()/(len(data)-1))
s_d
步骤四、计算统计量t,计算公式为 t = \frac{{\bar{d}-\mu}}{{\frac{{s_d}}{{\sqrt{n}}}}}
t = (d_bar)/(s_d/np.sqrt(len(data))) # 这里mu是0
t
#
计算p值
p_value = scipy.stats.t.sf(t, len(data)-1)
p_value
# 0.0007694243254842176
其中 \mu 为理论总体差值均值0,n为样本数。
结论 选择显著性水平 0.05 的话,p = 0.0007 < 0.05,故应该拒绝原假设。具体来说就是该结果倾向支持减肥前后的重量之差大于零(即减肥前重量大于减肥后,也就是有减肥效果)的备则假设。
同样的,我们用现成的函数 stats.ttest_rel,一步到位进行t检验,直接返回的就是t统计量和p值:
data = pd.read_table("./t-data/diet.txt",sep = ' ')
data.sample(5)
| before | after | | 58 | 50 | | 76 | 71 | | 69 | 65 | | 68 | 76 | | 81 | 75 |
a = data['before']
b = data['after']
stats.ttest_rel(a, b,alternative = 'greater')
# #配对T检验,检测两个样本的均值差异,输入的参数是样本的向量
# Ttest_relResult(statistic=3.3550474801424173, pvalue=0.000769424325484219)
结论 选择显著性水平 0.05 的话,p = 0.0007 < 0.05,故应该拒绝原假设。具体来说就是该结果倾向支持减肥前后的重量之差大于零(即减肥前重量大于减肥后,也就是有减肥效果)的备则假设。
F检验
F检验(F-test),最常用的别名叫做联合假设检验(英语:joint hypotheses test),此外也称方差比率检验、方差齐性检验。
用于: 判断两组数据方差是否存在显著差异。
步骤一:分别计算两组样本数据的均值 \bar{X}
步骤二:分别计算两组样本数据的标准方差的平方
S^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar{X})^2
步骤三:计算两组样本数据标准方差的平方比
F = \frac{max(s_1^2,s_2^2)}{min(s_1^2,s_2^2)} ,把平方大的作为分子,小的作为分母。
得到F值后根据两组数据的自由度和置信度查表对比,同样的,F值也是越小越说明差异性不显著。
stats模块中虽然没有f检验的函数,但是却有着f分布的生成函数,可以利用其进行f检验:
import numpy as np
from scipy.stats import f_oneway
# 创建两个样本
sample1 = np.array([1, 2, 3, 4, 5])
sample2 = np.array([2, 4, 6, 8, 10])
# 使用 f_oneway 函数进行 F 检验
f_statistic, p_value = f_oneway(sample1, sample2)
# 打印检验结果
print("F statistic:", f_statistic)
print("p-value:", p_value)
#在上述示例中,我们创建了两个样本 sample1 和 sample2,每个样本包含五个观测值。然后,我们使用 f_oneway 函数对这两个样本进行 F 检验。
#f_oneway 函数返回两个值,第一个是 F 统计量,第二个是对应的 p 值。我们可以根据 p 值来判断样本方差是否有显著差异。如果 p 值小于设定的显著性水平(通常为 0.05),则可以拒绝原假设,认为样本方差存在显著差异。
#在上述示例中,我们可以得到 F 统计量为 4.0,p 值为 0.078。由于 p 值大于 0.05,我们不能拒绝原假设,即无法认为这两个样本的方差存在显著差异。
#需要注意的是,在使用 f_oneway 函数进行 F 检验时,输入的样本应该是一维数组或列表形式。如果有多个样本,可以将它们作为函数的参数传入。
也可以引入sklearn进行f检验
# 例子1
from sklearn.datasets import make_classification
from sklearn.feature_selection import f_classif
# 生成样本数据集
X, y = make_classification(n_samples=1000, n_features=10, n_informative=5, n_redundant=5, random_state=42)
# F检验
F, pval = f_classif(X, y)
# 输出结果
print(F)
print(pval)
# 特征排序(如果不做机器学习可以忽略这一步)
indices = np.argsort(F)[-10:]
print(indices)
#这里我们生成了一个包含10个特征的样本分类数据集,其中5个特征包含区分两类信息,5个特征冗余。
#使用f_classif函数可以计算每个特征的F-score和p值,F-score越高表示该特征越重要。
#最后通过argsort排序,输出最重要的特征索引。
#F检验通过计算每个特征对目标类别的区分能力,来对特征重要性进行评估和排序,是一种常用的过滤式特征选择方法。
# 例子2
import numpy as np
from sklearn.feature_selection import f_regression
# 创建特征矩阵 X 和目标向量 y
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
y = np.array([1, 2, 3])
# 使用 f_regression 函数进行 F 检验
f_values, p_values = f_regression(X, y)
# 打印 F 统计量和 p 值
print("F values:", f_values)
print("p-values:", p_values)
例5.10(两总体方差之比的假设检验) 检验修完Python课程的学生是否比修完数据库课程的学生考CDA的成绩方差更大
某高校数据科学专业的学生,修完一门数据库课程的41名学生考CDA的方差s^2=120,修完Python课程的31名学生考CDA的方差是s^2=80,这些数据是否表明,修完数据库的学生要比修完Python的学生CDA成绩的方差更大?
分析过程:由于目标是希望修完Python的学生CDA成绩的方差更大,因此选择上侧检验。两总体方差之比用F检验,将方差较大的数据库课程的考试成绩视为总体1
于是我们有了原假设和备择假设
H_0: \sigma_1 < \sigma_2 \leftrightarrow H_1: \sigma_1 \geqslant \sigma_2 :
import numpy as np
from scipy import stats
def f_test_by_s_square(n1, n2, s1_square,s2_square, side ='two-sided'):
"""
参数
n1 :样本1的数量
n2 :样本2的数量
s1_square:样本1的方差
s2_square:样本2的方差
#
# F_value :F统计量的值
# p_value :对应的p值
"""
F_value = s1_square/s2_square
F = stats.f(dfn = n1-1, dfd = n2-1)
if side=='two-sided':
print("two-sided")
p_value = 2*min(F.cdf(F_value), 1-F.cdf(F_value))
return F_value,p_value
elif side=='greater':
print("greater")
p_value = 1-F.cdf(F_value)
return F_value,p_value
f_statistic , p_value= f_test_by_s_square(n1=41, n2=31,s1_square=120,s2_square=80,side='greater')# 打印检验结果
# 选择上侧检验所以side='greater'
print("F statistic:", f_statistic)
print("p-value:", p_value)
结论 选择显著性水平 0.05 的话,p = 0.1256 > 0.05,故无法原假设。结果无法支持修完数据库的学生要比修完Python的学生CDA成绩的方差更大的备则假设。
\chi^2检验
卡方检验(chi-square test),也就是χ2检验,是以 \chi^2 分布为基础的一种用途广泛的分析定性数据差异性的方法,通过频数进行检验。
之前假设检验一节中,我们知道卡方检验可以做指定方差和样本方差是否有差异

例5.5 检验某考试中心升级题库后考生分数的方差是否有显著变化
某数据分析师认证考试机构CDA考试中心,历史上的持证人考试分数的方差为 \sigma^2=100,现在升级了题库,该考试中心希望新型考题的方差保持在原有水平上,为了研究该问题,收集到了30份新考题的考分组成的样本,样本方差是\sigma^2=152,在 \alpha=0.05的显著性水平下进行假设检验。
分析过程:由于目标是希望考试分数的方差保持原有水平,因此选择双侧检验
于是我们有了原假设和备择假设
H_0: \sigma^2 =100 \leftrightarrow H_1:\sigma^2 \neq 100:
import numpy as np
from scipy import stats
def chi2test(sample_var, sample_num,sigma_square,side, alpha=0.05):
'''
参数:
sample_var--样本方差
sample_num--样本容量
sigma_square--H0方差
返回值:
pval
'''
chi_square =((sample_num-1)*sample_var)/(sigma_square)
p_value = None
if side == 'two-sided':
p = stats.chi2(df=sample_num-1).cdf(chi_square)
p_value = 2*np.min([p, 1-p])
elif side == 'less':
p_value = stats.chi2(df=sample_num-1).cdf(chi_square)
elif side == 'greater':
p_value = stats.chi2(df=sample_num-1).sf(chi_square)
return chi_square,p_value
p_value = chi2test(sample_var = 162, sample_num = 30, sigma_square = 100,side='two-sided')
print("p值:", p_value)
# p值: 0.07213100536907469
结论: 选择显著性水平 0.05 的话,P=0.0721 > 0.05, 故无法拒绝原假设。具体来说就是不支持方差发生了变化的备则假设。换句话说新题型的方差依然保持在原有水平上
那么,卡方检验还有什么应用呢?
统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,如果卡方值越大,二者偏差程度越大;反之,二者偏差越小;若两个值完全相等时,卡方值就为0,表明理论值完全符合。
卡方值计算公式:
\chi^2 = \sum_{i=1}^N \frac{(O_{ij} - E_{ij})^2}{E_{ij}}
①卡方优度检验 对一列数据进行统计检验,分析单个分类变量实际观测的比例与期望的比例是否一致。
②配对卡方 研究实验过程中,用不同方法检测同一批人,看两个方法的效果是否有显著差异。
③ 交叉表卡方
研究两组分类变量的关系:如性别与看不看直播是否有关系。
例7.5(交叉表卡方):性别与对待吸烟的态度之间的相关性 一项研究调查了不同性别的成年人对在公众场合吸烟的态度,结果如表所示。那么,性别与对待吸烟的态度之间的相关程度
python中stats模块,同样有卡方检验的计算函数
from scipy.stats import chi2_contingency
import numpy as np
data = np.array([[15,10], [10,26]])
chi2, p, dof, expected = chi2_contingency(data,correction =False)
print(f'卡方值={chi2}, p值={p}, 自由度={dof}')
# 卡方值=6.3334567901234555, p值=0.011848116168529757, 自由度=1
结论:p = 0.0118<0.05,拒绝原假设,表明两变量之间的正向关系很显著。
sklearn中的特征选择中也可以进行卡方检验。
from sklearn.feature_selection import chi2
import numpy as np
# 假设我们有一个包含100个样本和5个特征的数据集
X = np.random.randint(0, 10, (40, 5))
y = np.random.randint(0, 2, 40)
# 使用chi2函数计算特征变量与目标变量之间的卡方统计量和p值
chi2_stats, p_values = chi2(X, y)
# 打印每个特征的卡方统计量和p值
for i in range(len(chi2_stats)):
print(f"Feature {i+1}: chi2_stat = {chi2_stats}, p_value = {p_values}")
#在上面的例子中,我们生成了一个包含100个样本和5个特征的随机数据集。然后,我们使用chi2函数计算每个特征与目标变量之间的卡方统计量和p值。最后,我们打印出每个特征的卡方统计量和p值。
#根据卡方统计量和p值,我们可以判断每个特征与目标变量之间的关联程度。如果卡方统计量较大且p值较小,则说明特征与目标变量之间存在显著关联,可以考虑选择该特征作为重要的特征进行建模。
<hr/>至此,统计学的描述性统计、推断统计基本告一段落,剩下的贝叶斯、线性回归、逻辑回归请读者自行查阅资料进行学习,我们下个系列见!
(PS:可以在评价中写下你想学的系列,包括不限于SQL、Pandas、Julia、机器学习、数学建模、数据治理)
致谢
《统计学极简入门》图文系列教程的写作过程中参考了诸多经典书籍,包括:
人大统计学教授吴喜之老师的 《统计学:从数据到结论》;
浙大盛骤教授的 《概率论与数理统计》;
辛辛那提大学 David R. Anderson的 《商务经济与统计》;
北海道大学的马场真哉的 《用Python动手学统计学》 ;
千叶大学研究院教授栗原伸一的《统计学图鉴》;
前阿里巴巴产品专家徐小磊的知乎:磊叔-数据化运营;
知乎旧梦的文章T检验、F检验、卡方检验详细分析及应用场景总结;
csdn文章T检验、卡方检验、F检验;
以及CDA认证考试中心 提供的部分案例数据集
在此一并感谢以上内容的作者!
一死生为虚诞,齐彭殇为妄作。各位加油! 关注我(没有关注24小时就不能发消息了)私信”统计学代码“可以获取以上内容的ipnb代码
有统计学相关问题可以随时点击下方卡片咨询:
原文地址:https://zhuanlan.zhihu.com/p/334574642 |
 /3
/3 