如何简单得到一个单光子源——基于自发参量下转换的预示单光子产生

非诚勿扰孟非

在量子光学实验中，我们经常需要产生非经典光，尤其是单光子。一个非常自然的想法是利用单个粒子的二能级系统产生荧光单光子，即输入泵浦光让这个系统通过受激吸收从基态激发到激发态，等待有限时间后它就会自发辐射出一个光子。然而在很长的一段时间内，操控一个单粒子都是非常困难的，无论是用原子阱或离子阱操控单个原子或离子，还是在溶剂或聚合物中操控有机染料分子。前者往往需要复杂而巨大的实验装置，对于后者，尽管大分子可以直接用显微镜看到然后直接进行操控，装置简单了不少，但光漂白（photobleaching）效应的存在使得染料分子的荧光发射次数存在明显上限。直到21世纪以金刚石NV色心（nitrogen-vacancy center）为代表的带缺陷中心的固体材料系统的出现，稳定而易于操控的单光子源才逐渐在实验室中出现。
不过直到今天这种"真单光子源"仍然是略高大上的玩意，事实上，在实验室快乐搬砖的phd们通常并不需要真正物理上产生一个光子数态 |1\rangle 。我们有时更加关心光场的统计性质，也就是说，如果我们能制备出一个统计性质和单光子态近似一样的系统，那么同样可以认为它是一种单光子源。
用量子力学语言描述就是，考虑单模光场的密度算符：
\hat\rho=\sum_{m,n=0}^{\infty}\rho_{mn}|m\rangle\langle n|
我们希望 \rho_{11}\approx1,\rho_{mn}\ll1(m\not=1且n\not=1) 即可，这样考虑下面的实验：


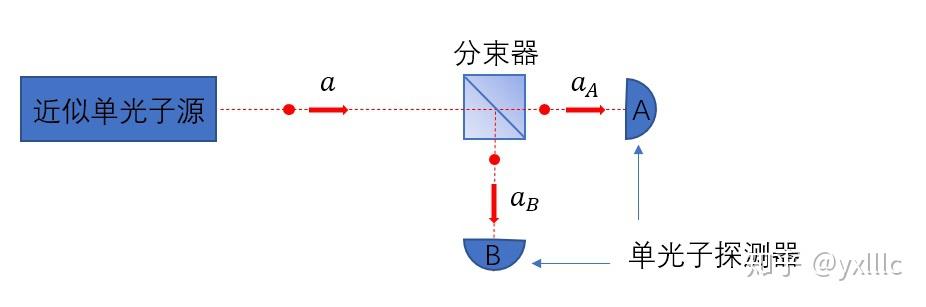
可以想象单光子源每次发出的单光子经过分束器要么透射被A探测到，要么反射被B探测到（假设探测器量子效率为100%），概率均为50%，不会有同时探测到信号的情况，即存在完全的反相关性（anticorrelation)。那么做二阶关联测量就会有：
g_{AB}^{(2)}=\frac{\langle a_A^\dagger a_B^\dagger a_Ba_A\rangle}{\langle a_A^\dagger a_A\rangle\langle a_B^\dagger a_B\rangle}=\frac{tr(\hat\rho a^{\dagger2} a^2)}{tr(\hat\rho a^\dagger a)^2}=\frac{\sum_{n=2}^\infty  n(n-1)\rho_{nn}}{(\sum_{n=1}^\infty  n\rho_{nn})^2}\approx0
首先，单纯衰减一个强光是不能得到单光子态的，比如对于相干态
|\alpha\rangle= \mathrm{e}^{- \frac{|\alpha|^2}{2}}\sum_{n=0}^{ \infty}\frac{\alpha^n}{\sqrt{n!}}|n\rangle
经过衰减算符 \hat U=\eta^{a^\dagger a} (0<\eta<1) 的作用后
\hat U|\alpha\rangle= \mathrm{e}^{- \frac{|\alpha|^2}{2}}\sum_{n=0}^{ \infty}\frac{\eta^n\alpha^n}{\sqrt{n!}}|n\rangle \propto|\eta\alpha\rangle
仍然是一个相干态，泊松分布的光子数统计没有改变。因此对于下面的实验：


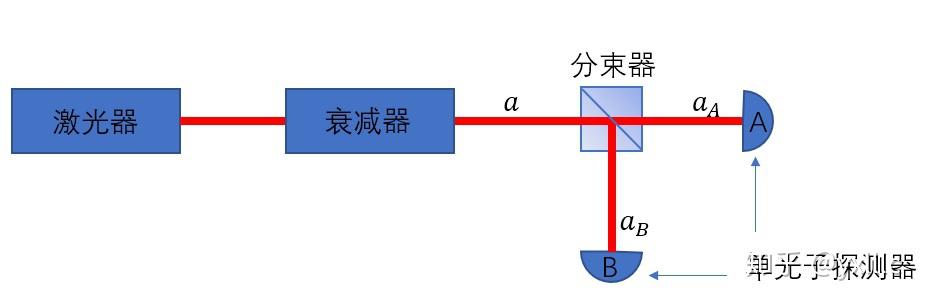
做二阶关联测量：
g_{AB}^{(2)}=\frac{\langle a_A^\dagger a_B^\dagger a_Ba_A\rangle}{\langle a_A^\dagger a_A\rangle\langle a_B^\dagger a_B\rangle}=\frac{\langle\eta\alpha|a^{\dagger2} a^2|\eta\alpha\rangle}{\langle\eta\alpha|a^\dagger a|\eta\alpha\rangle^2}=1
实际上可以进一步说明，任何线性光学方法均无法以经典光为输入得到非经典光（考虑
Glauber–Sudarshan P表象），自然也就不可能得到单光子态。
那么非线性光学呢？我们首先知道自发参量下转换（spontaneous parameter down conversion）可以产生纠缠光子对。考虑下面的实验：


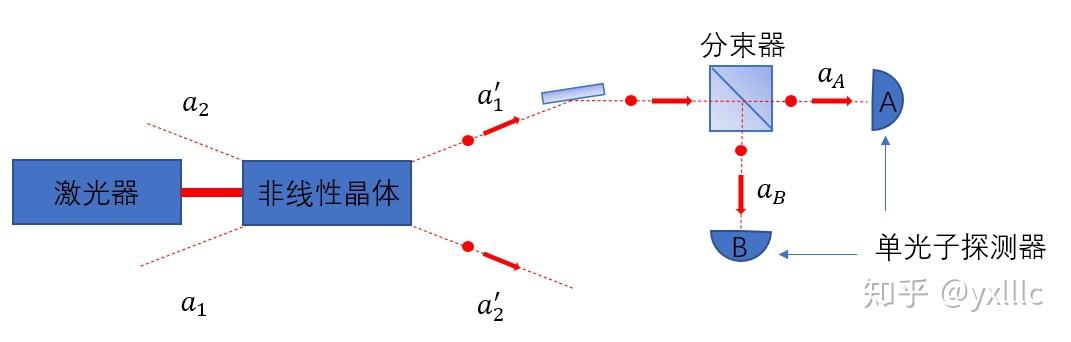
在激光器强度和相位匹配调节合适的情况下，SPDC对应的幺正演化算符可近似为：
\hat U=\mathrm{e}^{s(\mathrm{e}^{-\mathrm{i}\theta}a_1a_2-\mathrm{e}^{\mathrm{i}\theta}a_1^\dagger a_2^\dagger)} ，其中 s\ll1,0\le\theta<2\pi
那么对于路径1和2生成的光场可表示为：
|\psi\rangle= \hat U|00\rangle=\sum_{n=0}^\infty\sqrt{p_n}\mathrm{e}^{\mathrm{i}\phi_n}|nn\rangle ，其中 0<p_n<1,0\le\phi_n<2\pi
在泰勒展开并对每项做进一步展开后，对于每个光子数态 |nn\rangle_{12} ，它前面至少作用了 n 个 a_1^\dagger a_2^\dagger ，所以前面的系数 \sqrt{p_n}\mathrm{e}^{\mathrm{i}\phi_n}=\Theta(s^n) ，即 p_n=\Theta(s^{2n})
如果我们只考虑路径1的光子，它的约化密度算符为：
\hat{\rho_1}=tr_{2}(|\psi\rangle\langle\psi|)=\sum_{n=0}^\infty p_n|n\rangle\langle n|
那么 \rho_{00}=p_0=\Theta(1)\gg0 ,不满足近似单光子源的条件，做二阶关联测量就会有：
g_{AB}^{(2)}=\frac{\langle a_A^\dagger a_B^\dagger a_Ba_A\rangle}{\langle a_A^\dagger a_A\rangle\langle a_B^\dagger a_B\rangle}=\frac{tr_1(\hat\rho_1 a_1^{\dagger2} a_1^2)}{tr_1(\hat\rho_1 a_1^\dagger a_1)^2}=\frac{\sum_{n=2}^\infty  n(n-1)p_n}{(\sum_{n=1}^\infty  np_n)^2}\approx\frac{2p_2}{p_1^2}=\Theta(1)

用海森堡绘景我们可以精确计算出这个结果，即路径1和2上光场始终为0光子数态，但湮灭算符发生演化，即 a&#39;_1=\hat U^\dagger a_1\hat U 和 a&#39;_2=\hat U^\dagger a_2\hat U ，运用Baker-Hausdorff引理可以轻松得到：
a&#39;_1=\cosh(s)a_1-\mathrm{e}^{\mathrm{i}\theta}\sinh(s) a_2^\dagger
a&#39;_2=\cosh(s)a_2-\mathrm{e}^{\mathrm{i}\theta}\sinh(s) a_1^\dagger
那么
a&#39;_1|00\rangle=-\mathrm{e}^{\mathrm{i}\theta}\sinh(s)|01\rangle
{a&#39;_1}^2|00\rangle=\sqrt{2}\mathrm{e}^{2\mathrm{i}\theta}\sinh^2(s)|02\rangle
因此有：
g_{AB}^{(2)}=\frac{\langle a_A^\dagger a_B^\dagger a_Ba_A\rangle}{\langle a_A^\dagger a_A\rangle\langle a_B^\dagger a_B\rangle}=\frac{\langle00|{a&#39;_{1}}^{\dagger2} {a&#39;_1}^2|00\rangle}{\langle00|{a&#39;_{1}}^{\dagger} a&#39;_1|00\rangle}=2

事实上我们已经非常接近了，只要解决掉约化密度算符中 |0\rangle 的部分就好，也就是很大概率得不到任何光子的问题。既然这是纠缠光子对产生，一个自然的想法就产生了：我们可以通过测量路径2上的光子的存在来预示（herald）路径1上光子的必然出现。用量子力学语言描述就是我们构造一个投影测量
\hat M=\hat{I_1}\otimes a_2  
其中 \hat I 表示恒等算符，那么系统先经过测量 \hat M 再只考虑路径1光子得到的约化密度算符为：
\hat \rho_{1,heralded}=\frac{tr_{2}(\hat M|\psi\rangle\langle\psi|\hat{M}^\dagger)}{tr_{12}(\hat M|\psi\rangle\langle\psi|\hat{M}^\dagger)}=\frac{\sum_{n=1}^\infty np_n|n\rangle\langle n|}{\sum_{n=1}^\infty np_n}=|1\rangle\langle1|+\Theta(s^2)\hat \rho_{noise}
可以证明这是一个成功的单光子态近似，考虑下面的实验：


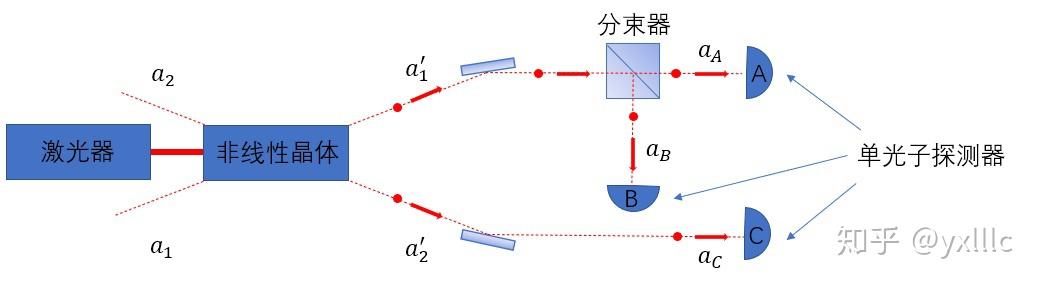
我们这时要做的是条件二阶关联测量，即在C探测到信号的条件下，对A和B做二阶关联测量，用概率论语言描述就是：
g_{AB|C}^{(2)}=\frac{P(AB|C)}{P(A|C)P(B|C)}=\frac{\frac{P(ABC)}{P(C)}}{\frac{P(AC)}{P(C)}\frac{P(BC)}{P(C)}}=\frac{P(ABC)P(C)}{P(AC)P(BC)}
那么换成量子力学语言描述就有：
g_{AB|C}^{(2)}=\frac{\langle a_A^\dagger a_B^\dagger a_C^\dagger a_C a_Ba_A\rangle\langle a_C^\dagger a_C\rangle}{\langle a_A^\dagger a_C^\dagger a_C a_A\rangle\langle a_B^\dagger a_C^\dagger a_C a_B\rangle}=\frac{tr_1(\hat\rho_1 a_1^{\dagger2} a_2^\dagger a_2 a_1^2)tr_1(\hat\rho_1a_2^\dagger a_2)}{tr_1(\hat\rho_1 a_1^\dagger a_2^\dagger a_2 a_1)^2}

=\frac{(\sum_{n=2}^\infty  n^2(n-1)p_n)(\sum_{n=1}^\infty np_n)}{(\sum_{n=1}^\infty  n^2p_n)^2}\approx\frac{2p_2}{p_1}=\Theta(s^2)\approx0
这种技术在实验量子光学中被称为预示单光子源技术。

同样用海森堡绘景我们可以精确计算出这个结果
a&#39;_2a&#39;_1|00\rangle=-\mathrm{e}^{\mathrm{i}\theta}\cosh(s)\sinh(s)|00\rangle+\mathrm{e}^{2\mathrm{i}\theta}\sinh^2(s)|11\rangle
a&#39;_2{a&#39;_1}^2|00\rangle=2\mathrm{e}^{2\mathrm{i}\theta}\cosh(s)\sinh^2(s)|01\rangle-\sqrt{2}\mathrm{e}^{3\mathrm{i}\theta}\sinh^3(s)|12\rangle
设 m=\sinh^2(s) ,则有：
g_{AC}^{(2)}=\frac{\langle a_A^\dagger a_C^\dagger a_Ca_A\rangle}{\langle a_A^\dagger a_A\rangle\langle a_C^\dagger a_C\rangle}=\frac{\langle00|{a&#39;_{1}}^{\dagger}{a&#39;_{2}}^{\dagger} a&#39;_2a&#39;_1|00\rangle}{\langle00|{a&#39;_{1}}^{\dagger} a&#39;_1|00\rangle\langle00|{a&#39;_{2}}^{\dagger} a&#39;_2|00\rangle}=2+\frac{1}{m}
g_{BC}^{(2)}=\frac{\langle a_B^\dagger a_C^\dagger a_Ca_B\rangle}{\langle a_B^\dagger a_B\rangle\langle a_C^\dagger a_C\rangle}=\frac{\langle00|{a&#39;_{1}}^{\dagger}{a&#39;_{2}}^{\dagger} a&#39;_2a&#39;_1|00\rangle}{\langle00|{a&#39;_{1}}^{\dagger} a&#39;_1|00\rangle\langle00|{a&#39;_{2}}^{\dagger} a&#39;_2|00\rangle}=2+\frac{1}{m}
g_{ABC}^{(3)}=\frac{\langle a_A^\dagger a_B^\dagger a_C^\dagger a_Ca_Ba_A\rangle}{\langle a_A^\dagger a_A\rangle\langle a_B^\dagger a_B\rangle\langle a_C^\dagger a_C\rangle}=\frac{\langle00|{a&#39;_{1}}^{\dagger2}{a&#39;_{2}}^{\dagger} a&#39;_2{a&#39;_1}^2|00\rangle}{\langle00|{a&#39;_{1}}^{\dagger} a&#39;_1|00\rangle^2\langle00|{a&#39;_{2}}^{\dagger} a&#39;_2|00\rangle}=4+\frac{6}{m}
所以有：
g_{AB|C}^{(2)}=\frac{g_{ABC}^{(3)}}{g_{AC}^{(2)}g_{BC}^{(2)}}=\frac{6m^2+4m}{(2m+1)^2}
当 s\ll1时 m\ll1 ， g_{AB|C}^{(2)}=\Theta(m)=\Theta(s^2)

参考文献

• Braig, C., Zarda, P., Kurtsiefer, C. et al. Experimental demonstration of complementarity with single photons . Appl Phys B 76, 113–116 (2003)
  

2. Kurtsiefer, Christian & Mayer, Sonja & Zarda, Patrick & Weinfurter, Harald. (2000). Stable Solid-State Source of Single Photons. Physical review letters. 85. 290-3.
3. Grangier, Ph & Roger, G. & Aspect, Alain. (1986). Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences. EPL (Europhysics Letters). 1. 173.

原文地址：https://zhuanlan.zhihu.com/p/259322969